题目内容
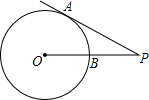
 如图:PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中错误的是( )
如图:PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中错误的是( )分析:根据切线长定理得出PA=PB,∠BPO=∠APO,根据等腰三角形性质推出OP⊥AB,根据以上结论推出即可.
解答:解:∵PA、PB是⊙O的切线,切点是A、B,
∴PA=PB,∠BPO=∠APO,
∴选项A、B错误;
∵PA=PB,∠BPO=∠APO,
∴OP⊥AB,∴选项C错误;
根据已知不能得出C是PO的中点,故选项D正确;
故选D.
∴PA=PB,∠BPO=∠APO,
∴选项A、B错误;
∵PA=PB,∠BPO=∠APO,
∴OP⊥AB,∴选项C错误;
根据已知不能得出C是PO的中点,故选项D正确;
故选D.
点评:本题考查了切线长定理和等腰三角形的性质的应用,熟练地运用性质进行推理是解此题的关键,题目比较典型,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为( )
如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为( )A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
 如图,PA切⊙O于点A,PBC是⊙O的割线,且PB=BC,如果PA=3
如图,PA切⊙O于点A,PBC是⊙O的割线,且PB=BC,如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
 如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )
如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 8、如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径等于( )
8、如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径等于( )