题目内容
13.把方程$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x+3)^{2}+{y}^{2}}}$=$\frac{1}{2}$化成整式方程,得( )| A. | x2+3y2+6x-9=0 | B. | x2+3y2-6x-9=0 | C. | x2+y2-2x-3=0 | D. | x2+y2+2x-3=0 |
分析 先将方程两边都平方即可去掉根号,再根据去分母化为整式方程,最后整理整式方程即可得.
解答 解:方程两边平方,得:$\frac{{x}^{2}+{y}^{2}}{(x+3)^{2}+{y}^{2}}=\frac{1}{4}$,
∴4(x2+y2)=(x+3)2+y2,
去括号,得:4x2+4y2=x2+6x+9+y2,
移项、合并,得:3x2+3y2-6x-9=0,
两边都除以3,得:x2+y2-2x-3=0,
故选:C.
点评 本题主要考查无理方程,无理方程转化为整式方程常用的方法有:乘方法,配方法,因式分解法,设辅助元素法,利用比例性质法等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,那小芳家的电话号码为5170928.
,那小芳家的电话号码为5170928.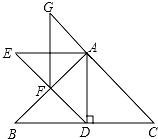 如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$.
如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$.