题目内容
3.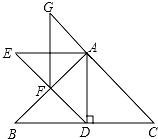 如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$.
如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$.
分析 通过直角三角形的性质特点,斜边上的高等于斜边的一半,再分析规律,便能计算出答案了.
解答 解:∵等腰直角△ABC直角边长为2,
∴斜边长为=2$\sqrt{2}$.,
斜边上的高也是斜边上的中线,应该等于斜边的一半.
那么第一个等腰直角三角形的腰长为$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$;
∴第二个等腰直角三角形的斜边长=$\sqrt{2×(\sqrt{2})^{2}}$=2,
∴第二个等腰直角三角形的腰长=$\frac{1}{2}$×2=1,
那么第n个等腰直角三角形的腰长为($\frac{\sqrt{2}}{2}$)n-1.
∴第n个等腰直角三角形的面积=$\frac{1}{2}$×[($\frac{\sqrt{2}}{2}$)n-1]2=$\frac{1}{{2}^{n}}$,
故答案是:$\frac{1}{{2}^{n}}$.
点评 此题考查了等腰直角三角形,解决本题的关键是根据等腰直角三角形的性质得到其他等腰直角三角形的表示规律.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
13.把方程$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x+3)^{2}+{y}^{2}}}$=$\frac{1}{2}$化成整式方程,得( )
| A. | x2+3y2+6x-9=0 | B. | x2+3y2-6x-9=0 | C. | x2+y2-2x-3=0 | D. | x2+y2+2x-3=0 |
 如图是一个圆锥的正视图,则该圆锥的侧面积是$\frac{\sqrt{7}}{2}$π.
如图是一个圆锥的正视图,则该圆锥的侧面积是$\frac{\sqrt{7}}{2}$π.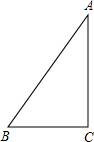 如图,在△ABC中,∠C=90°,BC=5,AB=13,则tanB的值为$\frac{12}{5}$.
如图,在△ABC中,∠C=90°,BC=5,AB=13,则tanB的值为$\frac{12}{5}$.