题目内容
15．
已知：如图，五边形ABCDE中，∠A=107°，∠B=121°，∠C=132°．求证：AE∥CD．
分析 根据五边形的内角和，可得∠AED与∠CDE的关系，根据平行线的判定，可得答案．
解答 证明：∵∠A+∠B+∠C+∠D+∠E=（5-2）×180°=540°，
∴∠D+∠E=540°-∠A-∠B-∠C=540°-107°-121°-132°=180°，
∴AE∥CD．
点评 本题考查了多边形的内角与外角，利用五边形的内角和得出（∠D+∠E）的度数是解题关键．
练习册系列答案
相关题目
6．下列计算正确的是（ ）
| A． | $\frac{7}{10}$×$\frac{8}{5}$=1 | B． | $\frac{4}{5}$÷5=4 | C． | （4$+\frac{1}{2}$）×$\frac{3}{4}$=4×$\frac{3}{4}$$+\frac{1}{2}$ | D． | $\frac{2}{3}$÷2=$\frac{1}{3}$ |
如图，△ABC中，AB=AC=6cm，∠BAC=120°，M、N分趴是AB，AC的中点，AD⊥BC，垂足为D，以D为圆心，3cm为半径画圆，判断A，B，C，M，N各点和⊙D的位置关系．
4．
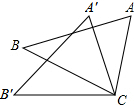如图，△ACB≌△A′CB，点A和点A′，点B和点B′是对应点，∠BCB′=30°，则∠ACA′的度数为（ ）
如图，△ACB≌△A′CB，点A和点A′，点B和点B′是对应点，∠BCB′=30°，则∠ACA′的度数为（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |