题目内容
10.在△ABC中,E、F、P分别在边BC、CA、AB上,已知AE、BF、CP相交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=1994,则$\frac{AD}{DE}$•$\frac{BD}{DF}$•$\frac{CD}{DP}$的值等于1996.分析 观察所求式子可知,直接进行线段比值推导明显很复杂,因此可考虑从面积的角度入手.不妨设S△ABD=S1,S△BDC=S2,SADC=S3,则$\frac{AD}{DE}$、$\frac{BD}{DF}$、$\frac{CD}{DP}$均可以用S1、S2、S3表示,三者相乘化简即可得结果.
解答 解:设S△ABD=S1,S△BDC=S2,SADC=S3,
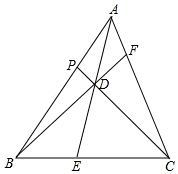
则$\frac{AD}{DE}=\frac{{S}_{ABD}}{{S}_{BDE}}$=$\frac{{S}_{△ADC}}{{S}_{△DEC}}$=$\frac{{S}_{△ABD}+{S}_{△ADC}}{{S}_{△BDE}+{S}_{△DEC}}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$,
同理:$\frac{BD}{DF}$=$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$,$\frac{CD}{DP}=\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$,
$\frac{AD}{DE}+\frac{BD}{DF}+\frac{CD}{DP}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$+$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$+$\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$=1994,
$\frac{AD}{DE}•\frac{BD}{DF}•\frac{CD}{DP}$=$\frac{{S}_{1}+{S}_{3}}{{S}_{2}}$•$\frac{{S}_{1}+{S}_{2}}{{S}_{3}}$•$\frac{{S}_{2}+{S}_{S}}{{S}_{1}}$=1994+2=1996.
点评 本题考查相似三角形的判定与性质及面积法,难度较大.在面对较复杂的线段比例问题时,借助面积法往往会使问题得以简化,这一点值得注意.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 身高180cm和身高90cm | B. | 向东走5公里和向南走5公里 | ||
| C. | 收入300元和支出300元 | D. | 使用汽油10公斤和浪费酒精10公斤 |
| A. | 其图象的开口向下 | B. | 其图象的对称轴为x=-3 | ||
| C. | 其最大值为1 | D. | 当x<3时,y随x的增大而减小 |

 如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2. 正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形.
正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形.