题目内容
13.已知A=4x2+ax-y+b,B=2bx2-x+5y-1,且A-2B的值与字母x的取值无关.则(a+b)2012=1.分析 把A与B代入A-2B中,去括号合并后,根据结果与x取值无关,确定出a与b的值,代入原式计算即可得到结果.
解答 解:∵A=4x2+ax-y+b,B=2bx2-x+5y-1,
∴A-2B=4x2+ax-y+b-2(2bx2-x+5y-1)=4x2+ax-y+b-4bx2+2x-10y+2=(4-4b)x2+(a+2)x-11y+b+2,
由结果与x的取值无关,得到4-4b=0,a+2=0,
解得:a=-2,b=1,
则原式=(-2+1)2012=(-1)2012=1.
故答案为:1
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.“十一”黄金周期间,某风景区在7天假期中,每天旅游的人数变化如下表(正数表示比前一天增加的人数,负数表示比前一天减少的人数)所示(单位:万人),若9月30日的游客人数为1万人.
(1)这7天内哪天游客的人数最多?哪天游客的人数最少?
(2)这7天内该风景区平均每天有游客多少人?
| 人数 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)这7天内该风景区平均每天有游客多少人?
8.通过计算填写下表:
请你根锯上表,直接写出a2+$\frac{1}{{a}^{2}}$与(a+$\frac{1}{a}$)2之间的数量关系;并验证当a=-$\frac{1}{2}$时,你得到的数量关系是否还成立.
| a | 2 | -$\frac{1}{3}$ | -1 |
| a2+$\frac{1}{{a}^{2}}$ | $\frac{17}{4}$ | $\frac{82}{9}$ | 2 |
| (a+$\frac{1}{a}$)2 | $\frac{25}{4}$ | $\frac{100}{9}$ | 4 |
2.某个体户经营香蕉,7月8日晚库存香蕉0千克,若进价是2.5元/千克.售价是3.3元/千克,7月9日至7月11日这三天销售情况如下表:
(1)第一天结束库存香蕉4千克,第二天结束库存香蕉1千克.
(2)①成本:购进量×进价=375.
②售出额:售出量×售价=452.1.
③损耗费用:损耗量×进价=22.5.
④库存费用:库存量×进价=22.5.
该个体户盈利了吗?请通过分析计算作答.
| 9日 | 10日 | 11日 | |
| 购进(千克) | 50 | 48 | 52 |
| 售出(千克) | 42 | 49 | 46 |
| 损耗(千克) | 4 | 2 | 3 |
(2)①成本:购进量×进价=375.
②售出额:售出量×售价=452.1.
③损耗费用:损耗量×进价=22.5.
④库存费用:库存量×进价=22.5.
该个体户盈利了吗?请通过分析计算作答.

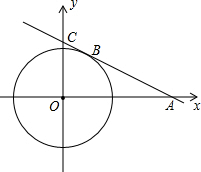 如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问:
如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问: