题目内容
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为
A. | B. | C. | D. |
D
解析试题分析:∵正方形ABCD,∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA。
∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°。∴∠ADO=∠BAA1。
∵∠DOA=∠ABA1,∴△DOA∽△ABA1。∴ 。
。
∵AB=AD= ,∴BA1=
,∴BA1= 。
。
∴第2个正方形A1B1C1C的边长A1C=A1B+BC= ,面积是
,面积是 。
。
同理第3个正方形的边长是 ,面积是:
,面积是: 。
。
第4个正方形的边长是 ,面积是
,面积是
…
第2012个正方形的边长是 ,面积是
,面积是 。
。
故选D。

练习册系列答案
相关题目
已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )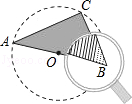
| A.∠A+∠B=900 | B.∠A=∠B |
| C.∠A+∠B>900 | D.∠A+∠B的值无法确定 |
小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
| A.10米 | B.12米 | C.15米 | D.22.5米 |
如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是
| A.b2=ac | B.b2=ce | C.be=ac | D.bd=ae |
如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于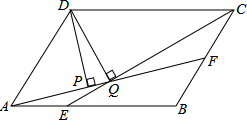
| A.3∶4 | B. ∶ ∶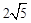 | C. ∶ ∶ | D. ∶ ∶ |
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则 的值为【 】
的值为【 】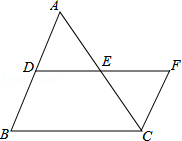
| A.1:3 | B.2:3 | C.1:4 | D.2:5 |



 在横杆
在横杆 的正上方,
的正上方, ,
, ,
, ,点
,点 的距离是3m,则点
的距离是3m,则点
 m
m


