题目内容
如图，在平行四边形ABCD中，AB=6，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且AB=3CF，DG⊥AE，垂足为G，若DG=2，则AE的边长为（ ）
A．4 | B．6 | C．6 | D．4 |
B.
解析试题分析：由AE为角平分线，得到∠DAE=∠BAE，再由ABCD为平行四边形，得到AB//CD，∠BAE=∠DFA；所以DA=DF；由AB=6，AB=3CF可知：CF=2、DF=DA=4；由DG⊥AE，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD=4、DG=2得
,所以
；由AB//CD，可得△ABE∽△FCE，所以
，解得：
，所以
.故选B.
考点：1、平行四边形的性质；2、等腰三角形的性质；3、勾股定理；4、相似三角形的判定与性质.
如图所示的两个三角形是位似图形，它们的位似中心是
| A．点O | B．点P | C．点M | D．点N |
如图，△ABC的三个顶点都在⊙O上，∠BAC的平分线交BC于点D，交⊙O于点E，则与△ABD相似的三角形有（ ）
| A．3个 | B．2个 | C．1个 | D．0个 |
如图，△ABC中，AD⊥BC于D，且有下列条件：（1）∠B＋∠DAC＝90°；（2）∠B＝∠DAC；（3）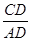
＝
；（4）AB2＝BD·BC其中一定能够判定△ABC是直角三角形的共有（ ）
| A．3个 | B．2个 | C．1个 | D．0个 |
如果
，那么
的值是( )
A． | B． | C． | D．5 |
如图，在Rt△ABC中，∠C=90°，P是斜边上一定点，过点P作直线与一直角边交于点Q使图中出现两个相似三角形，这样的点Q有 ( )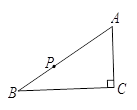
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，小华为了测量所住楼房的高度，他请来同学帮忙，测量了同一时刻他自己的影长和楼房的影长分别是0.5米和10米．已知小华的身高为1.6米，那么他所住楼房的高度______．
| A．8米 | B．16米 |
| C．32米 | D．48米 |
已知，AB是⊙O的直径，且C是圆上一点，小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B（如图所示），那么下列关于∠A与放大镜中的∠B关系描述正确的是（ ）
| A．∠A+∠B=900 | B．∠A=∠B |
| C．∠A+∠B＞900 | D．∠A+∠B的值无法确定 |
