题目内容
如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于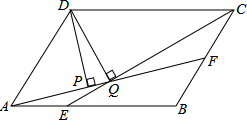
| A.3∶4 | B. ∶ ∶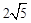 | C. ∶ ∶ | D. ∶ ∶ |
D
解析分析:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
∵根据三角形的面积和平行四边形的面积得: ,即
,即 。
。
∴AF×DP=CE×DQ,。
∵四边形ABCD是平行四边形,∴AD∥BC。
∵∠DAB=60°,∴∠CBN=∠DAB=60°。∴∠BFN=∠MCB=30°。
∵AB:BC=3:2,∴设AB=3a,BC=2a。
∵AE:EB=1:2,F是BC的中点,∴BF=a,BE=2a,BN= a,BM=a。
a,BM=a。
由勾股定理得:FN= a,CM=
a,CM= a。
a。
∴ 。
。
∴ 。∴
。∴ 。故选D。
。故选D。

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )
| A.∠A+∠B=900 | B.∠A=∠B |
| C.∠A+∠B>900 | D.∠A+∠B的值无法确定 |
如图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )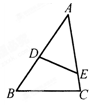
A. | B.7 | C.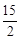 | D. |
如图,ABCD是边长为1的正方形,对角线AC所在的直线上有两点M、N,使∠MBN=1350,则MN的最小值是不是( )
A.1+ | B.2+ | C.3+ | D.2 |






 B.
B. C.
C. D.
D.

 OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】