题目内容
11.若关于x的一元二次方程kx2+2x-1=0有两个实数根,则k的取值范围是k≥-1且k≠0.分析 首先利用根的判别式△=b2-4ac=4+4k≥0,根据一元二次方程的意义得出k≠0,两者结合得出答案即可.
解答 解:∵关于x的一元二次方程kx2+2x-1=0有两个实数根,
∴△=b2-4ac=4+4k≥0,k≠0,
解得:k≥-1且k≠0.
故答案为:k≥-1且k≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及一元二次方程的意义.

练习册系列答案
相关题目
1.若单项式xm-nyn与4x2ny3的差是-3xm-ny3,则( )
| A. | m≠9 | B. | n≠3 | C. | m=9且n=3 | D. | m≠9且n≠3 |
20.现对某商品降价10%后进行促销,为了使销售总金额不变,则销售量比按原价销售时约应增加( )
| A. | 10% | B. | 11% | C. | 12% | D. | 13% |
 如图,CD是Rt△ABC斜边上的高,则图中相等的锐角有2对.
如图,CD是Rt△ABC斜边上的高,则图中相等的锐角有2对.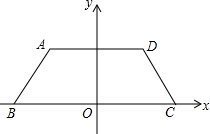 四边形ABCD在平面直角坐标系中的位置如图,已知AD∥BC,AB=CD,O是BC的中点,∠ABC=45°,AD=6,BC=10,顶点A的坐标是(-3,2),顶点C的坐标是(5,0).
四边形ABCD在平面直角坐标系中的位置如图,已知AD∥BC,AB=CD,O是BC的中点,∠ABC=45°,AD=6,BC=10,顶点A的坐标是(-3,2),顶点C的坐标是(5,0).