题目内容
2.解方程(组)(1)$\frac{1-2x}{3}=\frac{2x+1}{5}-2$
(2)$\left\{\begin{array}{l}{2x+y=3}\\{x-2y=4}\end{array}\right.$
(3)$\left\{\begin{array}{l}{2x+3x+z=11}\\{x+y+z=6}\\{3x-y-z=-2}\end{array}\right.$.
分析 (1)利用解一元一次方程的步骤与方法求得方程的解即可;
(2)利用加减消元法求得方程组的解即可;
(3)利用消元法把方程化为二元一次方程组,进一步求得方程组的解,代入原方程中的一个方程,进一步求得原方程组的解.
解答 解:(1)$\frac{1-2x}{3}=\frac{2x+1}{5}-2$
5(1-2x)=3(2x+1)-30
5-10x=6x+3-30
-10x-6x=3-30-5
-16x=-32
x=2;
(2)$\left\{\begin{array}{l}{2x+y=3①}\\{x-2y=4②}\end{array}\right.$
①×2+②得,5x=10,
解得:x=2,
代入①得,2×2+y=3,
解得:y=-1,
所以原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{2x+3y+z=11①}\\{x+y+z=6②}\\{3x-y-z=-2③}\end{array}\right.$,
①-②得,x+2y=5④,
②+③得,4x=4,
解得:x=1,
代入④得,1+2y=5,
解得:y=2,
把x=1,y=2代入②得,1+2+z=6,
解得:z=3,
所以原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$.
点评 此题考查解三元一次方程组,二元一次方程组,一元一次方程,掌握方法与步骤是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
13.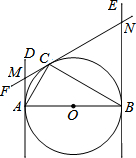 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
10.下面图形中,对称轴最多的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 半圆 | D. | 等腰梯形 |
7.下列说法正确的是( )
| A. | 一个角的余角只有一个 | |
| B. | 一个角的补角必大于这个角 | |
| C. | 钝角的补角一定是锐角 | |
| D. | 若两个角互为补角,则一个是钝角,一个是锐角 |
12.下列运用等式的性质,变形正确的是( )
| A. | 若x=y,则x-5=y+5 | B. | 若a=b,则ac=bc | C. | 若x=y,则$\frac{x}{m}=\frac{y}{m}$ | D. | 若a=b,则a-2=2-b |