题目内容
14.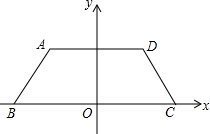 四边形ABCD在平面直角坐标系中的位置如图,已知AD∥BC,AB=CD,O是BC的中点,∠ABC=45°,AD=6,BC=10,顶点A的坐标是(-3,2),顶点C的坐标是(5,0).
四边形ABCD在平面直角坐标系中的位置如图,已知AD∥BC,AB=CD,O是BC的中点,∠ABC=45°,AD=6,BC=10,顶点A的坐标是(-3,2),顶点C的坐标是(5,0).
分析 过A作AE⊥BC于E,过D作DF⊥BC于F,于是得到四边形AEFD是矩形,由矩形的性质得到EF=AD=6,根据已知条件得到OB=OC=$\frac{1}{2}$BC=5,OE=$\frac{1}{2}$EF=3,根据等腰直角三角形的性质得到AE=BE=2,即可得到结论.
解答 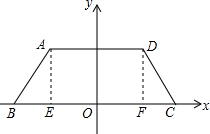 解:过A 作AE⊥BC于E,过D作DF⊥BC于F,
解:过A 作AE⊥BC于E,过D作DF⊥BC于F,
则四边形AEFD是矩形,
∴EF=AD=6,
∵AB=CD,O是BC的中点,
∴OB=OC=$\frac{1}{2}$BC=5,OE=$\frac{1}{2}$EF=3,
∴BE=2,
∵∠ABC=45°,
∴AE=BE=2,
∴顶点A的坐标是(-3,2),顶点C的坐标是(5,0).
故答案为:(-3,2),(5,0).
点评 本题考查了坐标与图形的性质,等腰梯形的性质,矩形的性质,等腰直角三角形的性质,正确的识图是解题的关键.

练习册系列答案
相关题目
12.下列运用等式的性质,变形正确的是( )
| A. | 若x=y,则x-5=y+5 | B. | 若a=b,则ac=bc | C. | 若x=y,则$\frac{x}{m}=\frac{y}{m}$ | D. | 若a=b,则a-2=2-b |
4.把二次函数y=x2的图象向右平移2个单位,再向下平移5个单位,所得图象对应的函数式是( )
| A. | y=(x-2)2-5 | B. | y=(x-2)2+5 | C. | y=(x+2)2-5 | D. | y=(x+2)2-5 |
 已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.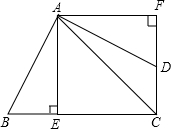 如图,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD的延长线于F.
如图,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD的延长线于F.