题目内容
17．计算：（1）$\sqrt{27}$-$\sqrt{12}$+$\sqrt{\frac{1}{3}}$；
（2）$a\sqrt{8a}+4{a^2}•\sqrt{\frac{1}{8a}}-\sqrt{2{a^3}}$．
分析 首先化为最简二次根式，再进一步合并得出答案即可．
解答 解：（1）原式=3$\sqrt{3}$-2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$
=$\frac{{4\sqrt{3}}}{3}$；
（2）原式=2a$\sqrt{2a}$+a$\sqrt{2a}$-a$\sqrt{2a}$
=2a$\sqrt{2a}$．
点评 此题考查二次根式的混合运算，掌握运算方法与化简的方法是解决问题的关键．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
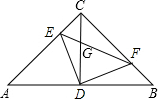如图，CD是等腰直角△ABC斜边上的高，E是AC上任意一点，DF⊥DE，交BC于F点．
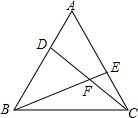如图，在等边三角形ABC中，D、E分别为AB、BC边上的两点，且AD=CE，求证：∠EBA=∠DCB．
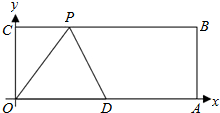已知：如图，O为坐标原点，四边形OABC为长方形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是等腰三角形时．
7．已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
如果x=a时，y＜0；那么x=a-1时，y的取值范围是$\frac{1}{3}$＜y＜$\frac{5}{3}$．
| x | … | -$\frac{1}{3}$ | 0 | $\frac{1}{3}$ | $\frac{2}{3}$ | 1 | $\frac{4}{3}$ | … |
| y | … | $\frac{5}{3}$ | $\frac{8}{9}$ | $\frac{1}{3}$ | 0 | -$\frac{1}{9}$ | 0 | … |