题目内容
2.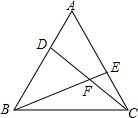 如图,在等边三角形ABC中,D、E分别为AB、BC边上的两点,且AD=CE,求证:∠EBA=∠DCB.
如图,在等边三角形ABC中,D、E分别为AB、BC边上的两点,且AD=CE,求证:∠EBA=∠DCB.
分析 根据SAS证明△CBE≌△ACD即可.
解答 证明:∵等边三角形ABC,
在△CBE与△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠CAD=60°}\\{AD=CE}\end{array}\right.$,
∴△CBE≌△ACD(SAS),
∴∠EBC=∠DCA,
∴∠EBA=∠DCB.
点评 本题主要考查了等边三角形的性质和全等三角形的判定与性质,熟悉等边三角形的性质和全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
7.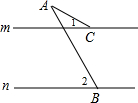 如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
 如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )| A. | 22° | B. | 25° | C. | 27° | D. | 30° |
12.下列各组数,能够作为直角三角形的三边长的是( )
| A. | 2,3,4 | B. | 4,5,7 | C. | 0.5,1.2,1.3 | D. | 12,36,39 |
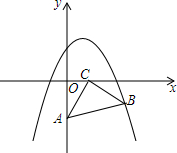 在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.
在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.