题目内容
7.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:| x | … | -$\frac{1}{3}$ | 0 | $\frac{1}{3}$ | $\frac{2}{3}$ | 1 | $\frac{4}{3}$ | … |
| y | … | $\frac{5}{3}$ | $\frac{8}{9}$ | $\frac{1}{3}$ | 0 | -$\frac{1}{9}$ | 0 | … |
分析 结合表格可得到抛物线与x轴的交点坐标、顶点坐标,结合图象得到a的范围,从而得到a-1的范围,结合表格即可解决问题.
解答 解:由表可知抛物线与x轴的两个交点为($\frac{2}{3}$,0)和($\frac{4}{3}$,0),
则抛物线的对称轴为x=$\frac{1}{2}$($\frac{2}{3}$+$\frac{4}{3}$)=1,
故顶点为(1,-$\frac{1}{9}$).
∵x=a时,y<0;
∴$\frac{2}{3}$<a<$\frac{4}{3}$,
∴-$\frac{1}{3}$<a-1<$\frac{1}{3}$,
∴x=a-1时,y的取值范围是$\frac{1}{3}$<y<$\frac{5}{3}$.
故答案为$\frac{1}{3}$<y<$\frac{5}{3}$.
点评 本题主要考查了抛物线的性质(对称轴、增减性等)、抛物线图象上点的坐标特征等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
18.“厉行勤俭节约,反对铺张浪费”势在必行,最新统计数据显示,中国每年浪费食物总量折合粮食大约是230000000人一年的口粮,将230000000用科学记数法表示为( )
| A. | 2.3×109 | B. | 0.23×109 | C. | 2.3×108 | D. | 23×107 |
12.下列各组数,能够作为直角三角形的三边长的是( )
| A. | 2,3,4 | B. | 4,5,7 | C. | 0.5,1.2,1.3 | D. | 12,36,39 |
16.下列函数中是二次函数的是( )
| A. | y=ax2+c | B. | y=x2+x | C. | y=(x-4)2-x2 | D. | y=x+2 |
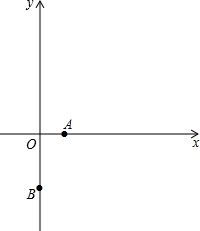 如图,抛物线y=-x2+5x+c经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+c经过点A(1,0),与y轴交于点B. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,