题目内容
2.已知二次函数y=x2-2x-1,求当-1≤x≤2时,函数的最大值与最小值.分析 先根据二次函数的已知条件,得出二次函数的图象开口向上,再根据变量x在-2≤x≤1的范围内变化,再分别进行讨论,即可得出函数y的最大值与最小值.
解答 解:∵二次函数y=x2-2x-1=(x-1)2-2,
∴该抛物线的对称轴为x=1,且a=1>0,
∴当-1时,二次函数有最大值为:(-1-1)2-2=2,
∴当x=10时,二次函数有最小值为-2,
综上所述,二次函数y=x2-2x-1,求当-1≤x≤2时,它的最大值为2,最小值为-2.
点评 本题考查了二次函数对称轴的求解,考查了二次函数的最值问题,本题中求得二次函数的对称轴是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
13.若k为任意实数,则抛物线y=-2(x-k)2+k2的顶点在( )
| A. | 抛物线y=x2上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
7.在坐标系中,以原点为圆心,以5为半径画圆,则点A(-3,4)的在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 不能确定 |
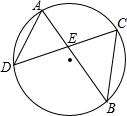 如图,AD=BC,求证:AB=DC,BE=DE.
如图,AD=BC,求证:AB=DC,BE=DE.