题目内容
1. 如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF是平行四边形;
(2)若AB=3cm,BC=5cm,∠B=60°,当AE=2cm时,四边形CEDF是菱形.
(直接写出答案,不需要说明理由)
分析 (1)易证得△CFG≌△EDG,推出FG=EG,根据平行四边形的判定即可证得结论;
(2)由∠B=60°,易得当△CED是等边三角形时,四边形CEDF是菱形,继而求得答案.
解答 (1)证明:四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
$\left\{\begin{array}{l}{∠FCG=∠EDG}\\{CG=DG}\\{∠CGF=∠DGE}\end{array}\right.$,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC=5cm,CD=AB=3cm,∠ADC=∠B=60°,
∵当DE=CE时,四边形CEDF是菱形,
∴当△CED是等边三角形时,四边形CEDF是菱形,
∴DE=CD=3cm,
∴AE=AD-DE=2cm,
即当AE=2cm时,四边形CEDF是菱形.
故答案为:2.
点评 此题考查了菱形的性质与判定、平行四边形的性质以及全等三角形的判定与性质.注意证得△CFG≌△EDG,△CED是等边三角形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年);
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据及统计量,对本公司的产品进行推销?(至少说两条)
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空
| 公司数值统计量 | 平均数 (单位:年) | 众数 (单位:年) | 中位数 (单位:年) |
| 甲公司 | 8 | 5 | 6 |
| 乙公司 | 9.6 | 8 | 8.5 |
| 丙公司 | 9.4 | 4 | 8 |
(3)如果你是丙公司的推销员,你将如何结合上述数据及统计量,对本公司的产品进行推销?(至少说两条)
16.如图,下面几何体的俯视图不是圆的是( )
| A. |  | B. |  | C. |  | D. |  |
10.计算:6x+7x的结果是( )
| A. | 13x | B. | 7x | C. | 6x | D. | x |
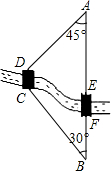 如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.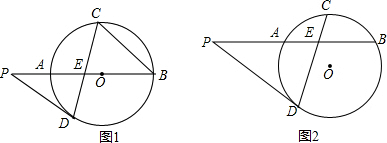
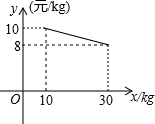 某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.
某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.