题目内容
5.计算:(1)(-4x)(2x2+3x-1)
(2)($\frac{2}{3}$ab2-2ab)•$\frac{1}{2}$ab
(3)(4ab-b2)(-2bc)
(4)(3x2y-xy2)•3xy
(5)2x(x2-$\frac{1}{2}$x+1)
(6)(-3x2)•(4x2-$\frac{4}{9}$x+1)
分析 (1)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案;
(2)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案;
(3)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案;
(4)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案;
(5)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案;
(6)直接利用单项式乘以多项式运算法则结合单项式乘以单项式运算法则求出答案.
解答 解:(1)(-4x)(2x2+3x-1)=-8x3-12x2+4x;
(2)($\frac{2}{3}$ab2-2ab)•$\frac{1}{2}$ab=$\frac{1}{3}$a2b3-a2b2;
(3)(4ab-b2)(-2bc)=-8ab2c+2b3c;
(4)(3x2y-xy2)•3xy=9x3y2-3x2y3;
(5)2x(x2-$\frac{1}{2}$x+1)=2x3-x2+2x;
(6)(-3x2)•(4x2-$\frac{4}{9}$x+1)=-12x2+$\frac{4}{3}$x3-3x2.
点评 此题主要考查了单项式乘以多项式,正确掌握运算法则结合运算符号求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )| A. | ac<0 | B. | b<0 | ||
| C. | b2-4ac<0 | D. | x=3关于x方程ax2+bx+c=0一个根 |
17.在反比例函数y=-$\frac{3}{2x}$中.自变量x的取值范围是( )
| A. | x>0 | B. | x<0 | C. | x≠0 | D. | x≥0 |
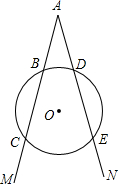 如图所示,射线AM交一圆于点B,C,射线AN交该圆于点D,F,且BC=DE,求证:AC=AE.
如图所示,射线AM交一圆于点B,C,射线AN交该圆于点D,F,且BC=DE,求证:AC=AE. 如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.
如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.