题目内容
13. 如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.
如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.(1)求原矩形的长和宽的比;
(2)求两矩形的相似比.
分析 (1)设原矩形的长边是a,短边是b,根据原矩形的长:宽=剩下矩形的长:宽列出算式,求值即可;
(2)根据(1)中结论和相似多边形的性质得到答案.
解答 解:(1)设原矩形的长边是a,短边是b,那么剪去的正方形的边长是b,剩下的矩形的长边是b,短边是a-b,由题意得,
a:b=b:(a-b),
∴a2-ab-b2=0,
用公式法解关于a的方程得,
a=$\frac{\sqrt{5}+1}{2}$b,a=$\frac{1-\sqrt{5}}{2}$b(舍去),
∴原矩形的长和宽的比为$\frac{\sqrt{5}+1}{2}$;
(2)两矩形的相似比为:$\frac{\sqrt{5}+1}{2}$.
点评 本题考查相似多边形的性质,掌握相似多边形的对应边相等、对应角相等是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
8.两种移动电话计费式表:
(1)根据题意,一个月内在本地通话时间如下,请填下表
(2)当通话时间是多少时,使用两种移动电话费用一样?
(3)什么情况下,使用神州行?什么情况下,使用全球通?
| 全球通 | 神州行 | |
| 月租费 | 50元/月 | 0 |
| 本地通话费 | 0.40元/分 | 0.60元/分 |
| 时间(分) | 80 | 120 | x |
| 全球通费用 | 82 | 98 | 50+0.4x |
| 神州行费用 | 48 | 72 | 0.6x |
(3)什么情况下,使用神州行?什么情况下,使用全球通?
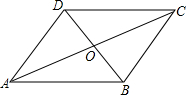 如图,平行四边形ABCD中,AC=12,BD=10,AB=m,则m的取值范围为1<x<11.
如图,平行四边形ABCD中,AC=12,BD=10,AB=m,则m的取值范围为1<x<11.