题目内容
3.已知BD、CE分别是△ABC的AC边、AB边上的高,M是BC边的中点,分别联结MD、ME、DE.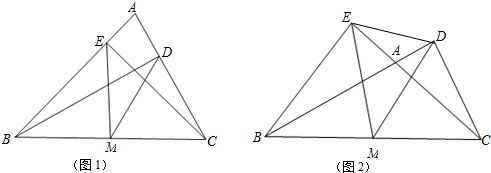
(1)当∠BAC<90°时,垂足D、E分别落在边AC、AB上,如图1,求证:DM=EM.
(2)若∠BAC=135°,试判断△DEM的形状,简写解答过程.
(3)当∠BAC>90°时,设∠BAC的度数为x,∠DME的度数为y,求y与x之间的函数关系式.
分析 (1)根据已知条件知,MD是Rt△BCD斜边BC上的中线,ME是Rt△BCE斜边BC上的中线,所以根据直角三角形斜边上的中线的性质进行证明即可;
(2)根据等腰三角形的性质得到∠DBM=∠BDM,∠MEC=∠MCE,由三角形的外角的性质得到∠BME=2∠BCE,∠CMD=2∠DBM,根据三角形的内角和得到∠DBC+∠ECM=45°,即可得到结论;
(3)根据等腰三角形的性质得到∠DBM=∠BDM,∠MEC=∠MCE,由三角形的外角的性质得到∠BME=2∠BCE,∠CMD=2∠DBM,根据三角形的内角和得到∠DBC+∠ECM=180°-x,根据平角的定义即可得到结论.
解答 (1)证明:∵BD、CE是△ABC的两条高,M是BC的中点,
∴在Rt△BDC中,MD是斜边BC上的中线,
∴MD=$\frac{1}{2}$BC;
同理,得
ME=$\frac{1}{2}$BC,
∴ME=MD;
(2)∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=2∠BCE,∠CMD=2∠DBM,
∵∠BAC=135°,
∴∠DBC+∠ECM=45°,
∴∠BME+∠CMD=90°,
∴∠DME=90°,
∴△DEM是等腰直角三角形;
(3)∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=2∠BCE,∠CMD=2∠DBM,
∵∠BAC=x,
∴∠DBC+∠ECM=180°-x,
∴∠BME+∠CMD=360°-2x,
∴∠DME=180°-(∠BME+∠CMD)=2x-180°,
即y=2x-180°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的判定,三角形的内角和,三角形外角的性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{-a+5}{-a-5}=\frac{a+5}{a-5}$ | B. | $\frac{1}{-x+6}=\frac{-1}{x+6}$ | ||
| C. | $\frac{-x+y}{-x-y}=-\frac{x-y}{x+y}$ | D. | $\frac{-x}{y-3x}=\frac{x}{3x-y}$ |
| A. | x=0 | B. | x1=0,x2=3 | C. | x=3 | D. | x1=1,x2=3 |
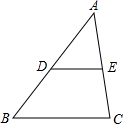 如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )
如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )| A. | 1:2 | B. | 1:4 | C. | 4:1 | D. | 2:1 |
| A. | (3,-2) | B. | (-2,3) | C. | (2,-3) | D. | (2,-3) |
 如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )| A. | 城 | B. | 市 | C. | 卫 | D. | 生 |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.