题目内容
11．方程x-3=x（x-3）的解为（ ）| A． | x=0 | B． | x1=0，x2=3 | C． | x=3 | D． | x1=1，x2=3 |
分析 先移项，再提公因式得到（x-3）（1-x）=0，原方程可化为x-3=0或x-1=0，然后解一次方程即可．
解答 解：∵x-3=x（x-3），
∴x-3-x（x-3）=0，
∴（x-3）（1-x）=0，
∴x-3=0或x-1=0，
∴x1=1，x2=3．
故选D．
点评 本题考查了因式分解法解一元二次方程，当把方程通过移项把等式的右边化为0后方程的左边能因式分解时，一般情况下是把左边的式子因式分解，再利用积为0的特点解出方程的根．因式分解法是解一元二次方程的一种简便方法，要会灵活运用．
练习册系列答案
单元期中期末卷系列答案
相关题目
1．“某幼儿园给小朋友分苹果，若每个小朋友分3个则剩1个；若每个小朋友分4个则少2个，问有多少个小朋友？”若设共有x个小朋友，则列出的方程是（ ）
| A． | 3x-1=4x+2 | B． | 3x+1=4x-2 | C． | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D． | $\frac{x+1}{3}$=$\frac{x-2}{4}$ |
如图：图①、图②都是4×4的正方形网格，小正方形的边长均为1，每个小正方形的顶点称为格点．在①、②两个网格中分别标注了5个格点，按下列要求画图：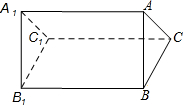
如图是一个三棱柱的图形，它共有五个面，其中三个面是长方形，两个面是三角形，请写出符合下列条件的棱（说明：每个空只需写出一条即可）．
