题目内容
15.已知x=$\frac{\sqrt{5}-1}{2}$,且x5=a+b$\sqrt{5}$,这里a,b均为有理数,则a+b=-3.分析 根据x的值计算出x2的值,将x5分解成x2•x2•x计算其值,根据题意可得a、b的值,进而可得答案.
解答 解:∵x=$\frac{\sqrt{5}-1}{2}$,
∴x2=$\frac{(\sqrt{5}-1)^{2}}{4}=\frac{6-2\sqrt{5}}{4}=\frac{3-\sqrt{5}}{2}$,
∴x5=x2•x2•x=($\frac{3-\sqrt{5}}{2}$)2•$\frac{\sqrt{5}-1}{2}$=-$\frac{19}{4}$+$\frac{7}{4}\sqrt{5}$,
又∵x5=a+b$\sqrt{5}$,且a,b均为有理数,
∴a=-$\frac{19}{4}$,b=$\frac{7}{4}$,
则a+b=-$\frac{19}{4}$+$\frac{7}{4}$=-3,
故答案为:-3.
点评 本题主要考查因式分解的应用能力,这里利用因式分解达到降幂目的是解题关键,对有理数性质得掌握是解题的根本.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
8.一元二次方程x2-1=0的根是( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | ±1 |




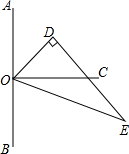 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.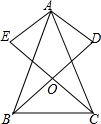 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.