题目内容
15．
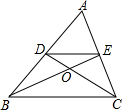如图，在△ABC中，两条中线BE，CD相交于点O，则S△DOE：S△DCE=（ ）| A． | 1：4 | B． | 1：3 | C． | 1：2 | D． | 2：3 |
分析 先根据题意判断出DE是△ABC的中位线，故可得出△ODE∽△OCB，由此可得出$\frac{OD}{OC}$=$\frac{1}{2}$，进而可得出结论．
解答 解：∵在△ABC中，两条中线BE，CD相交于点O，
∴DE是△ABC的中位线，
∴△ODE∽△OCB，
∴$\frac{OD}{OC}$=$\frac{1}{2}$，
∴$\frac{OD}{CD}$=$\frac{1}{3}$，
∵△DOE与△DCE等高，
∴S△DOE：S△DCE=OD：CD=1：3．
故选B．
点评 本题考查的是相似三角形的判定与性质，先根据题意得出DE是△ABC的中位线是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
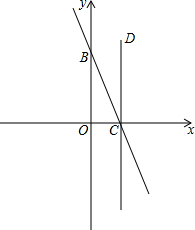如图，直线y=-2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．
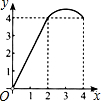
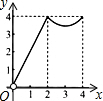
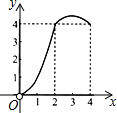
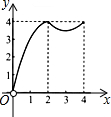
如图，正方形ABCD的边长为4，点P、Q分别是CD、AD的中点，动点E从点A向点B运动，到点B时停止运动；同时，动点F从点P出发，沿P→D→Q运动，点E、F的运动速度相同．设点E的运动路程为x，△AEF的面积为y，能大致刻画y与x的函数关系的图象是（ ）
