题目内容
1.若一等腰三角形的腰长为10,底边长为关于x的方程x2-14x+48=0的两根.(1)求出底边长,并作出该三角形(工具不限);
(2)若有一个圆能将该等腰三角形完全覆盖住,请问该圆的半径的最小值是多少?
分析 (1)利用因式分解法解方程得出即可,再利用三边作三角形即可;
(2)利用垂径定理以及勾股定理分别得出该圆的半径的最小值即可.
解答 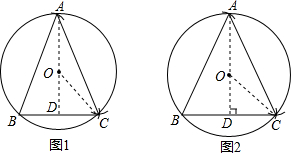 解:(1)x2-14x+48=0
解:(1)x2-14x+48=0
(x-8)(x-6)=0,
解得:x1=6,x2=8,
故底边为6或8;
(2)如图1,过点A作AD⊥BC于点D,连接CO,
当三边为6、10、10时,
则DC=3,故AD=$\sqrt{91}$,
设CO=x,则DO=$\sqrt{91}$-x,
故x2=($\sqrt{91}$-x)2+32,
解得:x=$\frac{50\sqrt{91}}{91}$,
故此时最小半径为:$\frac{50\sqrt{91}}{91}$;
如图2,过点A作AD⊥BC于点D,连接CO,
当三边为8、10、10时,
则DC=4,故AD=2$\sqrt{21}$,
设CO=x,则DO=2$\sqrt{21}$-x,
故x2=(2$\sqrt{21}$-x)2+42,
解得:x=$\frac{25\sqrt{21}}{21}$,
故此时最小半径为:$\frac{25\sqrt{21}}{21}$.
点评 此题主要考查了复杂作图以及垂径定理、勾股定理等知识,熟练应用垂径定理得出半径长是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.若分式$\frac{{x}^{2}-1}{{x}^{2}+x-2}$的值为0,则x的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±2 |
11.数据0,1,1,3,3,4的平均数和方差分别是( )
| A. | 2和1.6 | B. | 2和2 | C. | 2.4和1.6 | D. | 2.4和2 |
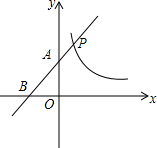 如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.
如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.