题目内容
11．
如图是用4个相同的小长方形与1个小正方形镶嵌而成的图案，已知该图案的面积为25，小正方形的面积为4，若用x，y表示小长方形的两邻边长（x＞y），则下列关系中不正确的是（ ）| A． | x+y=5 | B． | y-x=2 | C． | 4xy+4=25 | D． | y2+x2=25 |
分析 本题中正方形图案的边长7，同时还可用（x+y）来表示，其面积从整体看是25，从组合来看，可以是（x+y）2，还可以是（4xy+4），接下来，我们再灵活运用等式的变形，即可作出判断．
解答 解：A、因为正方形图案的边长5，同时还可用（x+y）来表示，故x+y=5正确；
B、因为正方形图案面积从整体看是25，
从组合来看，可以是（x+y）2，还可以是（4xy+4），
所以有（x+y）2=25，4xy+4=25
即xy=$\frac{21}{4}$，
所以（x-y）2=（x+y）2-4xy=25-21=4，
即x-y=2；
C、由B可知4xy+4=25，正确；
D、x2+y2=（x+y）2-2xy=25-2×$\frac{21}{4}$=$\frac{29}{2}$，故x2+y2=25是错误的．
故选D．
点评 本题考查整式的混合计算，关键是结合图形，利用等式的变形来解决问题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知抛物线y=-x2+2与x轴交于A、B两点，与y轴交于C点．
2．下列图案中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
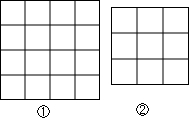如图，每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点，分别按下列要求画三角形：
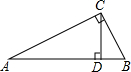已知：如图，△ABC中，∠ACB=90°，CD⊥AB于D，AB=8，BC=3．求：sin∠ACD的值及AD的长．
如图是有几个小立方体块搭建成的几何体的俯视图，小正方体中的数字表示在该位置小立方体块的个数，请画出从正面和从左面看到的这个几何体的形状图．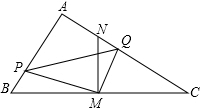
如图，在Rt△ABC中，∠BAC=90°，∠ABC=60°，AB=4$\sqrt{3}$，M是BC边的中点，MN⊥BC交AC于点N．直角∠PMQ绕顶点M旋转，使得边MP于线段BA交于点P，边MQ与线段AC交于点Q．