题目内容
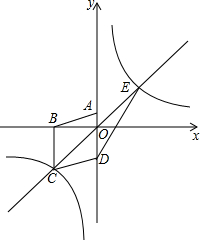 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于| 1 |
| 2 |
考点:反比例函数综合题
专题:
分析:过点A作∠BAD的平分线AF交x轴于点F,过点F作FG⊥AB于点G,求得点E的坐标后利用待定系数法确定直线的解析式即可.
解答: 解:设直线l与x轴交于点E,过点A作∠BAD的平分线AF交x轴于点F,过点F作FG⊥AB于点G,
解:设直线l与x轴交于点E,过点A作∠BAD的平分线AF交x轴于点F,过点F作FG⊥AB于点G,
∵∠DAE=
∠ABC,∠AEO=90°-∠DAE=90°
∠ABC=
(180°-∠ABC)=
∠BAD,
∴∠AEO=
∠BAD=∠DAF,
由题意得:OA=3,OB=4,
∴AB=5,AG=3,OF=GF,BG=2,cos∠ABO=
=
=
,
∴BF=
,
∴OF=
,tan∠AEO=tan∠DAF=
=
,
∴
=
,
∴OE=6,
①当E(6.0)时直线的解析式为y=
x+3;
②当E(-6.0)时直线的解析式为y=-
x+3.
 解:设直线l与x轴交于点E,过点A作∠BAD的平分线AF交x轴于点F,过点F作FG⊥AB于点G,
解:设直线l与x轴交于点E,过点A作∠BAD的平分线AF交x轴于点F,过点F作FG⊥AB于点G,∵∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEO=
| 1 |
| 2 |
由题意得:OA=3,OB=4,
∴AB=5,AG=3,OF=GF,BG=2,cos∠ABO=
| OB |
| AB |
| 4 |
| 5 |
| BG |
| BF |
∴BF=
| 5 |
| 2 |
∴OF=
| 3 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
∴
| AO |
| OE |
| 1 |
| 2 |
∴OE=6,
①当E(6.0)时直线的解析式为y=
| 1 |
| 2 |
②当E(-6.0)时直线的解析式为y=-
| 1 |
| 2 |
点评:本题考查了反比例函数的综合知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AD是△ABC的中线,
如图,AD是△ABC的中线, 如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.