题目内容
 如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.考点:等腰三角形的性质
专题:
分析:设∠EDC=x,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADE+x=∠B+∠BAD,∠AED=∠C+x,然后整理即可得解.
解答:解:设∠EDC=x,
由三角形的外角性质得,∠ADE+x=∠B+∠BAD,∠AED=∠C+x,
∵∠ADE=∠AED,
∴∠C+x+x=∠B+∠BAD,
∵∠B=∠C,
∴x=
∠BAD=
×30°=15°,
即∠EDC=15°.
由三角形的外角性质得,∠ADE+x=∠B+∠BAD,∠AED=∠C+x,
∵∠ADE=∠AED,
∴∠C+x+x=∠B+∠BAD,
∵∠B=∠C,
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
即∠EDC=15°.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记三角形的外角性质列出等式是解题的关键.

练习册系列答案
相关题目
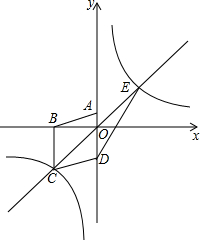 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于