题目内容
解方程:
+
+…+
=
.
| 1 | ||||
|
| 1 | ||||
(
|
| 1 | ||||
(
|
| 5 |
| 69 |
考点:二次根式的应用
专题:
分析:首先将已知方程化简,进而解无理方程求出即可.
解答:解:
+
+…+
=
∵
=
(
-
)
=
(
-
)
故原式可变为:
×(
-
)+
(
-
)+…+
(
-
)=
,
则
(
-
)=
,
整理可得出:
=
,
故
(
+20)=69,
解得:
=3或
=-23(不合题意舍去),
故x=9,
检验得x=9是原方程的根.
| 1 | ||||
|
| 1 | ||||
(
|
| 1 | ||||
(
|
| 5 |
| 69 |
∵
| 1 | ||||
|
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||||
(
|
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
故原式可变为:
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 5 |
| 69 |
则
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 5 |
| 69 |
整理可得出:
| 20 | ||||
|
| 20 |
| 69 |
故
| x |
| x |
解得:
| x |
| x |
故x=9,
检验得x=9是原方程的根.
点评:此题主要考查了分式方程的解法以及二次根式的化简求值,正确将原式化简成最简方程是解题关键.

练习册系列答案
相关题目
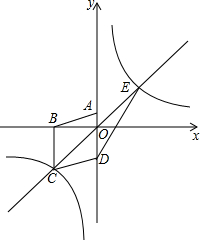 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于