题目内容
代数式2x2-3x+4最小值为 .
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:此题考查了配方法.在配方时要注意若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,可以先提取二次项系数,再配方,根据任何数的完全平方一定是非负数即可求解.
解答:解:2x2-3x+4=2(x2-
x)+4=2(x2-
x+
-
)+2=2[(x-
)2-
]+4=2(x-
)2+
,
∵(x-
)2≥0
∴代数式2x2-3x+4的最小值为
.
故答案为:
.
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 16 |
| 9 |
| 16 |
| 3 |
| 2 |
| 9 |
| 16 |
| 3 |
| 2 |
| 23 |
| 8 |
∵(x-
| 3 |
| 2 |
∴代数式2x2-3x+4的最小值为
| 23 |
| 8 |
故答案为:
| 23 |
| 8 |
点评:此题考查了配方法,解题的关键是将此题配方.

练习册系列答案
相关题目
若实数a≠b,且a,b满足a2-8a+5=0,b2-8b+5=0,则代数式
+
的值为( )
| b-1 |
| a-1 |
| a-1 |
| b-1 |
| A、-20 | B、2 |
| C、2或-20 | D、2或20 |
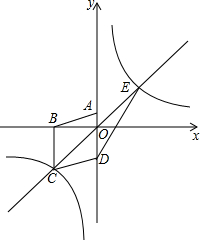 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).是否存在经过点A的直线l,使得直线l与y轴所夹锐角等于