题目内容
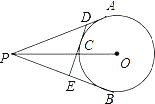
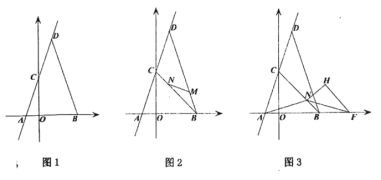
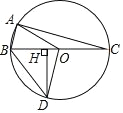
【题目】如图,⊙O 是△ABC 的外接圆,BC 是直径,AC=2DH,过点 D 作 DH 垂直BC 于点 H,以下结论中:①BH=HD;②∠BAO=∠BOD;③![]() ;④连接 AO、BD,若 BC=8,sin∠HDO=
;④连接 AO、BD,若 BC=8,sin∠HDO=![]() ,则四边形 ABDO 的面积为
,则四边形 ABDO 的面积为![]() , 其中正确的结论是 ____(请填写序号)
, 其中正确的结论是 ____(请填写序号)
【答案】②③
【解析】
作 OE⊥AC 于 E.首先证明 Rt△DOH≌Rt△AOE≌Rt△COE,利用全等三角形的性质,解直角三角形等知识一一判断即可.
作 OE⊥AC 于 E.
∵OE⊥AC,
∴AE=EC,
∵AC=2DH,
∴DH=AE=CE,
∵OD=OA=OC,
∴Rt△DOH≌Rt△AOE≌Rt△COE,
∴∠ODH=∠OAC,OH=OE,
∵BC 是直径,
∴∠BAC=90°,
∴∠BAO+∠OAE=90°,∵∠BOD+∠ODH=90°,
∴∠BAO=∠BOD,故②正确,
假设①成立,则点 H 与 O 重合,显然不符合题意,故①错误;
∵AE=EC,BO=OC,
∴AB=2OE=2OH,
∴![]() ,故③正确,
,故③正确,
∵BC=8,sin∠ODH= ![]() ,
,
∴OH=OE=1,
∴AE=EC=DH= ![]() ,
,
∴S△AOB=2S△AOE=2×![]() ×
×![]() ×1=
×1=![]() ,
,
∵S△BOD= ![]() ×4×
×4×![]() =2
=2![]() ,
,
∴S 四边形 ABDO=S△ABO+S△OBD=![]() +2
+2 ![]() =3
=3![]() .故④错误, 故答案为②③.
.故④错误, 故答案为②③.

【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级 | 中位数(分) | 众数(分) | 平均数(分) |
一班 | 85 | ||
二班 | 100 | 85 |
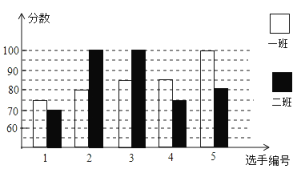
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?