题目内容
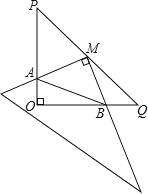
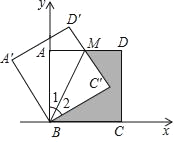
【题目】如图，将边长为
的正方形绕点B逆时针旋转30°，那么图中点M的坐标为（ ）
A.（，1）B.（1，）C.（，
）D.（，）
【答案】B
【解析】
由正方形和旋转的性质得出AB＝BC'＝
，∠BAM＝∠BC'M＝90°，证出Rt△ABM≌Rt△C'BM，得出∠1＝∠2，求出∠1＝∠2＝30°，在Rt△ABM中，求出AM的长即可．
解：∵四边形ABCD是正方形，
∴AB＝BC'＝，∠BAM＝∠BC'M＝90°，
在Rt△ABM和Rt△C'BM中，
，
∴Rt△ABM≌Rt△C'BM（HL），
∴∠1＝∠2，
∵将边长为的正方形绕点B逆时针旋转30°，
∴∠CBC'＝30°，
∴∠1＝∠2＝30°，
在Rt△ABM中，AB＝，∠1＝30°，
∴AB＝AM＝，
∴AM＝1，
∴点M的坐标为（1，）；
故选B．
练习册系列答案
名校课堂系列答案
相关题目
