ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсИКАыжсНЛгкЕу
жсИКАыжсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсе§АыжсНЛгкЕу
жсе§АыжсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсе§АыжсЩЯвЛЕуЃЌСЌНг
жсе§АыжсЩЯвЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ48ЃЎ
ЕФУцЛ§ЮЊ48ЃЎ
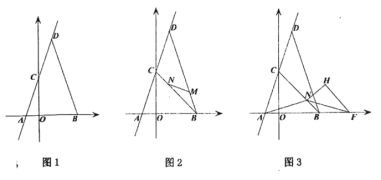
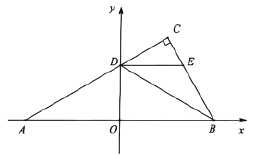
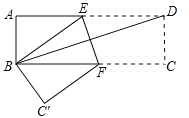
(1)ШчЭМ1ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
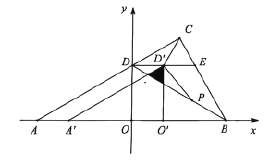
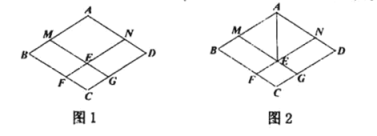
(2)ШчЭМ2ЃЌЕу![]() ЗжБ№дкЯпЖЮ
ЗжБ№дкЯпЖЮ![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪН(ВЛвЊЧѓаДГіздБфСП
ЕФКЏЪ§ЙиЯЕЪН(ВЛвЊЧѓаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇ)ЃЛ
ЕФШЁжЕЗЖЮЇ)ЃЛ
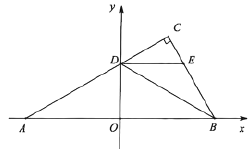
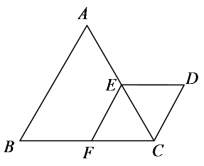
(3)дк(2)ЕФЬѕМўЯТЃЌШчЭМ3ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсе§АыжсЩЯЕу
жсе§АыжсЩЯЕу![]() гвВрвЛЕуЃЌЕу
гвВрвЛЕуЃЌЕу![]() ЮЊЕквЛЯѓЯоФквЛЕуЃЌ
ЮЊЕквЛЯѓЯоФквЛЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌжБЯп
ЩЯвЛЕуЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() КЭЕу
КЭЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЧыФуХаЖЯЫФБпаЮ
ЃЌЧыФуХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ6ЃЌ0ЃЉЃЛЃЈ2ЃЉdЃН![]() ЃЛЃЈ3ЃЉЫФБпаЮ
ЃЛЃЈ3ЃЉЫФБпаЮ![]() ЪЧОиаЮЃЌРэгЩМћНтЮі
ЪЧОиаЮЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉзїDLЁЭyжсДЙзуЮЊLЕуЃЌDIЁЭABДЙзуЮЊIЃЌжЄУїЁїDLCЁеЁїAOCЃЌЧѓЕУDЃЈ2ЃЌ12ЃЉЃЌдйгЩSЁїABDЃН![]() ABDIЃН48ЃЌЧѓЕУOBЃНABAOЃН82ЃН6ЃЌМДПЩЧѓBзјБъЃЛ
ABDIЃН48ЃЌЧѓЕУOBЃНABAOЃН82ЃН6ЃЌМДПЩЧѓBзјБъЃЛ
ЃЈ2ЃЉЩшЁЯMNBЃНЁЯMBNЃНІСЃЌзїNKЁЭxжсДЙзуЮЊKЃЌMQЁЭABДЙзуЮЊQЃЌMPЁЭNKЃЌДЙзуЮЊPЃЛжЄУїЫФБпаЮMPKQЮЊОиаЮЃЌдйжЄУїЁїMNPЁеЁїMQBЃЌЧѓГіBDЕФНтЮіЪНЮЊyЃН3xЃЋ18ЃЌMQЃНdЃЌАбyЃНdДњШыyЃН3xЃЋ18ЕУdЃН3xЃЋ18ЃЌБэДяГіOQЕФжЕЃЌдйгЩOQЃНOKЃЋKQЃНtЃЋdЃЌПЩЕУdЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉзїNWЁЭABДЙзуЮЊWЃЌжЄУїЁїANWЁеЁїCAOЃЌИљОнБпЕФЙиЯЕЧѓЕУNЃЈ4ЃЌ2ЃЉЃЛбгГЄNWЕНYЃЌЪЙNWЃНWYЃЌзїNSЁЭYFЃЌдйжЄУїЁїFHNЁеЁїFSNЃЌПЩЕУSFЃНFH=![]() ЃЌNYЃН2ЃЋ2ЃН4ЃЛЩшYSЃНaЃЌFYЃНFNЃНaЃЋ
ЃЌNYЃН2ЃЋ2ЃН4ЃЛЩшYSЃНaЃЌFYЃНFNЃНaЃЋ![]() ЃЌдкRtЁїNYSКЭRtЁїFNSжаРћгУЙДЙЩЖЈРэЧѓЕУFNЃЛдкRtЁїNWFжаЃЌРћгУЙДЙЩЖЈРэЧѓГіWFЃН6ЃЌЕУЕНFЃЈ10ЃЌ0ЃЉЃЛЩшGFНЛyжсгкЕуTЃЌЩшFNЕФНтЮіЪНЮЊyЃНpxЃЋqЃЈpЁй0ЃЉАбFЃЈ10ЃЌ0ЃЉNЃЈ4ЃЌ2ЃЉДњШыМДПЩЧѓГіжБЯпFNЕФНтЮіЪНЃЌСЊСЂЗНГЬзщЕУЕНGЕузјБъЃЛАбGЕуДњШыЕУЕНyЃН
ЃЌдкRtЁїNYSКЭRtЁїFNSжаРћгУЙДЙЩЖЈРэЧѓЕУFNЃЛдкRtЁїNWFжаЃЌРћгУЙДЙЩЖЈРэЧѓГіWFЃН6ЃЌЕУЕНFЃЈ10ЃЌ0ЃЉЃЛЩшGFНЛyжсгкЕуTЃЌЩшFNЕФНтЮіЪНЮЊyЃНpxЃЋqЃЈpЁй0ЃЉАбFЃЈ10ЃЌ0ЃЉNЃЈ4ЃЌ2ЃЉДњШыМДПЩЧѓГіжБЯпFNЕФНтЮіЪНЃЌСЊСЂЗНГЬзщЕУЕНGЕузјБъЃЛАбGЕуДњШыЕУЕНyЃН![]() x+3ЃЌПЩжЊRЃЈ4ЃЌ0ЃЉЃЌжЄУїЁїGRAЁеЁїEFRЃЌПЩЕУЫФБпаЮAGFEЮЊЦНааЫФБпаЮЃЌдйгЩЁЯAGFЃН180ЁуЁЯCGFЃН90ЁуЃЌПЩжЄУїЦНааЫФБпаЮAGFEЮЊОиаЮЃЎ
x+3ЃЌПЩжЊRЃЈ4ЃЌ0ЃЉЃЌжЄУїЁїGRAЁеЁїEFRЃЌПЩЕУЫФБпаЮAGFEЮЊЦНааЫФБпаЮЃЌдйгЩЁЯAGFЃН180ЁуЁЯCGFЃН90ЁуЃЌПЩжЄУїЦНааЫФБпаЮAGFEЮЊОиаЮЃЎ
НтЃКЃЈ1ЃЉСюxЃН0ЃЌyЃН6ЃЌСюyЃН0ЃЌxЃН2ЃЌ
ЁрAЃЈ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ6ЃЉЃЌ
ЁрAOЃН2ЃЌCOЃН6ЃЌ
зїDLЁЭyжсДЙзуЮЊLЕуЃЌDIЁЭABДЙзуЮЊIЃЌ
ЁрЁЯDLOЃНЁЯCOAЃН90ЁуЃЌЁЯDCLЃНЁЯACOЃЌDCЃНACЃЌ
ЁрЁїDLCЁеЁїAOCЃЈAASЃЉЃЌ
ЁрDLЃНAOЃН2ЃЌ
ЁрDЕФКсзјБъЮЊ2ЃЌ
АбxЃН2ДњШыyЃН3xЃЋ6ЕУyЃН12ЃЌ
ЁрDЃЈ2ЃЌ12ЃЉЃЌ
ЁрDIЃН12ЃЌ
ЁпSЁїABDЃН![]() ABDIЃН48ЃЌ
ABDIЃН48ЃЌ
ЁрABЃН8ЃЛ
ЁпOBЃНABAOЃН82ЃН6ЃЌ
ЁрBЃЈ6ЃЌ0ЃЉЃЛ

ЃЈ2ЃЉЁпOCЃНOBЃН6ЃЌ
ЁрЁЯOCBЃНЁЯCBOЃН45ЁуЃЌ
ЁпMNЃНMBЃЌ
ЁрЩшЁЯMNBЃНЁЯMBNЃНІСЃЌ
зїNKЁЭxжсДЙзуЮЊKЃЌMQЁЭABДЙзуЮЊQЃЌMPЁЭNKЃЌДЙзуЮЊPЃЛ
ЁрЁЯNKBЃНЁЯMQKЃНЁЯMPKЃН90ЁуЃЌ
ЁрЫФБпаЮMPKQЮЊОиаЮЃЌ
ЁрNKЁЮCOЃЌMQЃНPKЃЛ
ЁпЁЯKNBЃН90Ёу45ЁуЃН45ЁуЃЌ
ЁрЁЯMNKЃН45ЁуЃЋІСЃЌЁЯMBQЃН45ЁуЃЋІСЃЌ
ЁрЁЯMNKЃНЁЯMBQЃЌ
ЁпMNЃНMBЃЌЁЯNPMЃНЁЯMQBЃН90ЁуЃЌ
ЁрЁїMNPЁеЁїMQBЃЈAASЃЉЃЌ
ЁрMPЃНMQЃЛ
ЁпBЃЈ6ЃЌ0ЃЉЃЌDЃЈ2ЃЌ12ЃЉЃЌ
ЁрЩшBDЕФНтЮіЪНЮЊyЃНkxЃЋbЃЈkЁй0ЃЉЃЌ
Ёр![]() ЃЌНтЕУЃКk=-3ЃЌb=18ЃЌ
ЃЌНтЕУЃКk=-3ЃЌb=18ЃЌ
ЁрBDЕФНтЮіЪНЮЊyЃН3xЃЋ18ЃЌ
ЁпЕуMЕФзнзјБъЮЊdЃЌ
ЁрMQ=MPЃНdЃЌАбyЃНdДњШыyЃН3xЃЋ18ЕУdЃН3xЃЋ18ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрOQЃН![]() ЃЛ
ЃЛ
ЁпNЕФКсзјБъЮЊtЃЌ
ЁрOKЃНtЃЌ
ЁрOQЃНOKЃЋKQЃНtЃЋdЃЌ
Ёр![]() ЃНtЃЋdЃЌ
ЃНtЃЋdЃЌ
ЁрdЃН![]() ЃЛ
ЃЛ

ЃЈ3ЃЉзїNWЁЭABДЙзуЮЊWЃЌ
ЁрЁЯNWOЃН90ЁуЃЌ
ЁпЁЯACNЃН45ЁуЃЋЁЯACOЃЌЁЯANCЃН45ЁуЃЋЁЯNAOЃЌ
ЁпЁЯACOЃНЁЯNAOЃЌ
ЁрЁЯACNЃНЁЯANCЃЌ
ЁрACЃНANЃЌ
гжЁпЁЯACOЃНЁЯNAOЃЌЁЯAOCЃНЁЯNOWЃН90ЁуЃЌ
ЁрЁїANWЁеЁїCAOЃЈAASЃЉЃЌ
ЁрAOЃНNWЃН2ЃЌ
ЁрWBЃНNWЃН2ЃЌ
ЁрOWЃНOBWBЃН62ЃН4ЃЌ
ЁрNЃЈ4ЃЌ2ЃЉЃЛ
бгГЄNWЕНYЃЌЪЙNWЃНWYЃЌ
ЁрЁїNFWЁеЁїYFWЃЈSASЃЉ
ЁрNFЃНYFЃЌЁЯNFWЃНЁЯYFWЃЌ
гжЁпЁЯHFNЃН2ЁЯNFOЃЌ
ЁрЁЯHFNЃНЁЯYFNЃЌ
зїNSЁЭYFЃЌ
ЁпЁЯFHЁЭNHЃЌ
ЁрЁЯH
ЁпFNЃНFNЃЌ
ЁрЁїFHNЁеЁїFSNЃЈAASЃЉЃЌ
ЁрSFЃНFHЃН![]() ЃЌNYЃН2ЃЋ2ЃН4ЃЌ
ЃЌNYЃН2ЃЋ2ЃН4ЃЌ
ЩшYSЃНaЃЌFYЃНFNЃНaЃЋ![]() ЃЌ
ЃЌ
дкRtЁїNYSКЭRtЁїFNSжаЃКNS2ЃНNY2YS2ЃЛNS2ЃНFN2FS2ЃЛNY2YS2ЃНFN2FS2ЃЌ
Ёр42a2ЃН(aЃЋ![]() )2-(
)2-(![]() )2ЃЌ
)2ЃЌ
НтЕУaЃН![]()
ЁрFNЃН![]() ЃЛ
ЃЛ
дкRtЁїNWFжаWFЃН![]() ЃЌ
ЃЌ
ЁрFOЃНOWЃЋWFЃН4ЃЋ6ЃН10ЃЌ
ЁрFЃЈ10ЃЌ0ЃЉЃЌ
ЁрAWЃНAOЃЋOWЃН2ЃЋ4ЃН6ЃЌ
ЁрAWЃНFWЃЌ
ЁпNWЁЭAFЃЌ
ЁрNAЃНNFЃЌ
ЁрЁЯNFAЃНЁЯNAFЃЌ
ЁпЁЯACOЃНЁЯNAOЃЌ
ЁрЁЯNFAЃНЁЯACOЃЌ
ЩшGFНЛyжсгкЕуTЃЌЁЯCTFЃНЁЯACOЃЋЁЯCGFЃНЁЯCOFЃЋЁЯGFOЃЌ
ЁрЁЯCGFЃНЁЯCOFЃН90ЁуЃЌ
ЩшFNЕФНтЮіЪНЮЊyЃНpxЃЋqЃЈpЁй0ЃЉЃЌАбFЃЈ10ЃЌ0ЃЉNЃЈ4ЃЌ2ЃЉДњШыyЃНpxЃЋq
ЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрСЊСЂ ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
АбGЕуДњШыyЃНmxЃЋ3ЃЌЕУ![]() ЃЌЕУmЃН
ЃЌЕУmЃН![]() ЃЌ
ЃЌ
ЁрyЃН![]() xЃЋ3ЃЌ
xЃЋ3ЃЌ
СюyЃН0ЕУ0ЃН![]() xЃЋ3ЃЌxЃН4ЃЌ
xЃЋ3ЃЌxЃН4ЃЌ
ЁрRЃЈ4ЃЌ0ЃЉЃЌ
ЁрARЃНAOЃЋORЃН2ЃЋ4ЃН6ЃЌRFЃНOFORЃН104ЃН6ЃЌ
ЁрARЃНRFЃЌ
ЁпFEЁЮACЃЌ
ЁрЁЯFEGЃНЁЯAGEЃЌЁЯGAFЃНЁЯEFAЃЌ
ЁрЁїGRAЁеЁїEFRЃЈAASЃЉЃЌ
ЁрEFЃНAGЃЌ
ЁрЫФБпаЮAGFEЮЊЦНааЫФБпаЮЃЌ
ЁпЁЯAGFЃН180ЁуЁЯCGFЃН180Ёу90ЁуЃН90ЁуЃЌ
ЁрЦНааЫФБпаЮAGFEЮЊОиаЮЃЎ