题目内容
向△ABC外作正方形ACFG与ABDE,过A作BC的垂线AH,H为垂足,AH与EG交于P点.求证:AP=
BC.
| 1 |
| 2 |
考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:作EM∥AG交AP延长线于M,连接GM,利用两直线平行同旁内角互补得到一对角互补,再由周角定义及正方形现在得到一对角互补,利用同角的补角相等得到一对角相等,再利用同角的余角相等得到一对角相等,利用正方形的性质得到夹边相等,利用ASA得到三角形AEM与三角形BAC全等,利用全等三角形的对应边相等得到EM=AC,AM=BC,根据AC=AG,等量代换得到EM=AG,再由EM与AG平行,利用一组对边平行且相等的四边形为平行四边形,得到AEMG为平行四边形,根据平行四边形的对角线互相平分得到AP=
AM,等量代换即可得证.
| 1 |
| 2 |
解答: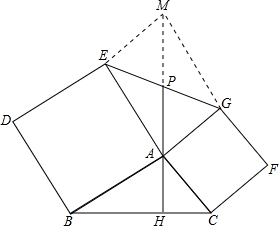 证明:作EM∥AG交AP延长线于M,连接GM,
证明:作EM∥AG交AP延长线于M,连接GM,
∴∠AEM+∠EAG=180°,
∵∠EAG+∠BAC=360°-∠BAE-∠CAG=180°,
∴∠AEM=∠BAC,
∵AH⊥MC,
∴∠BAH+∠ABH=90°,
∵∠EAM+∠BAH=180°-∠BAE=90°,
∴∠EAM=∠ABH,
在△AEM和△BAC中,
,
∴△AEM≌△BAC(ASA),
∴EM=AC,AM=BC,
∵AC=AG,
∴EM=AG,
∵EM∥AG,
∴AGME是平行四边形,
∴AP=
AM,
∴AP=
BC.
 证明:作EM∥AG交AP延长线于M,连接GM,
证明:作EM∥AG交AP延长线于M,连接GM,∴∠AEM+∠EAG=180°,
∵∠EAG+∠BAC=360°-∠BAE-∠CAG=180°,
∴∠AEM=∠BAC,
∵AH⊥MC,
∴∠BAH+∠ABH=90°,
∵∠EAM+∠BAH=180°-∠BAE=90°,
∴∠EAM=∠ABH,
在△AEM和△BAC中,
|
∴△AEM≌△BAC(ASA),
∴EM=AC,AM=BC,
∵AC=AG,
∴EM=AG,
∵EM∥AG,
∴AGME是平行四边形,
∴AP=
| 1 |
| 2 |
∴AP=
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,平行四边形的判定与性质,以及平行线的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
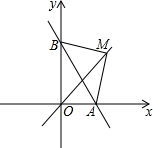 如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a-2)2+
如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a-2)2+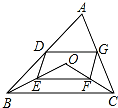 点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形. 如图所示,已知长方形ABCD的面积为20
如图所示,已知长方形ABCD的面积为20