题目内容
有下列关于x的两个方程:(1)x2+px+n=0;(2)x2+mx+q=0;已知方程(1)的两根是1和m+1,方程(2)的两根是2和n-1,解方程x2+px+q=0.
考点:根与系数的关系
专题:计算题
分析:先根据根与系数的关系得到1+m+1=-p①,1•(m+1)=n②,2+n-1=-m③,2(n-1)=q④,再利用解方程组的方法先计算出m与n,然后求出p与q的值,最后利用因式分解法解方程x2+px+q=0.
解答:解:根据题意得1+m+1=-p①,1•(m+1)=n②,2+n-1=-m③,2(n-1)=q④,
由③④解得m=-1,n=0,
所以p=-1,q=-2,
则方程x2+px+q=0变形为方程x2-x-2=0,
(x-2)(x+1)=0,
所以x1=2,x2=-1.
由③④解得m=-1,n=0,
所以p=-1,q=-2,
则方程x2+px+q=0变形为方程x2-x-2=0,
(x-2)(x+1)=0,
所以x1=2,x2=-1.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
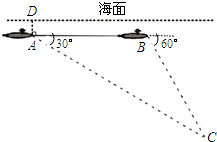 如图,我国一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,
如图,我国一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,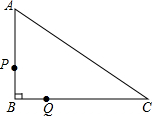 如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm)
如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm) 以各小正方形的顶点为顶点的三角形称为格点三角形,如图中的△ABC,请在图中画出与△ABC相似但不全等的三角形.
以各小正方形的顶点为顶点的三角形称为格点三角形,如图中的△ABC,请在图中画出与△ABC相似但不全等的三角形.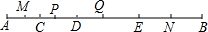 如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)
如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)