题目内容
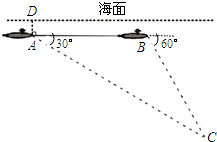 如图,我国一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,
如图,我国一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,(1)求海底黑匣子C点处距离海面的深度;
(2)若核潜艇的速度为2000米/时,核潜艇在B点处继续前行,求核潜艇再前行多长时间与黑匣子最近.(结果保留根号)
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)易证∠BAC=∠BCA,所以有BA=BC.然后在直角△BCE中,利用正弦函数求出CE;
(2)首先求出BE的长,进而利用核潜艇的速度为2000米/时,求出时间即可.
(2)首先求出BE的长,进而利用核潜艇的速度为2000米/时,求出时间即可.
解答: 解:(1)如图所示:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:(1)如图所示:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
=2000
(米).
∴CF=CE+EF=2000
+500(米).
答:海底黑匣子C点处距离海面的深度约为(2000
+500)米;
(2)∵BC=2000
,∠EBC=60°,
∴BE=2000
×cos60°=1000
(m),
故
=
(小时),
答:核潜艇再前行
小时与黑匣子最近.
 解:(1)如图所示:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:(1)如图所示:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
| ||
| 2 |
| 3 |
∴CF=CE+EF=2000
| 3 |
答:海底黑匣子C点处距离海面的深度约为(2000
| 3 |
(2)∵BC=2000
| 3 |
∴BE=2000
| 3 |
| 3 |
故
1000
| ||
| 2000 |
| ||
| 2 |
答:核潜艇再前行
| ||
| 2 |
点评:本题考查了仰俯角问题,解决此类问题的关键是正确的将仰俯角转化为直角三角形的内角并选择正确的边角关系解直角三角形,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 如图,在△ABC中,∠A=45°,∠B=70°,则外角∠ACD=
如图,在△ABC中,∠A=45°,∠B=70°,则外角∠ACD=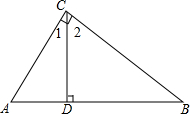 如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,写出分别与∠1,∠2相等的角,并说明理由.
如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,写出分别与∠1,∠2相等的角,并说明理由.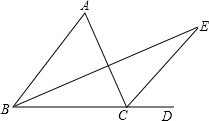 如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=
如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=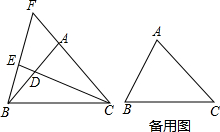 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.