题目内容
 如图,在等边△ABC中,D是AC的中点,延长BC至E,使CE=AD.
如图,在等边△ABC中,D是AC的中点,延长BC至E,使CE=AD.(1)请说明线段BD与DE的数量关系,并予以证明;
(2)若将“D是AC的中点”改为“D是AC上任意一点”,其他条件不变,BD与DE的数量关系如何?请画图证明.
考点:等边三角形的性质,等腰三角形的性质
专题:
分析:(1)根据等边三角形三线合一的性质可得∠CBD=30°,∠ACB=60°,根据CD=CE可得∠CDE=∠CED,根据∠CDE+∠CED=∠ACB即可解题;
(2)过E作EF∥BA交AC的延长线于F点,根据等边三角形的性质得到∠A=∠ACB=60°,AB=AC,则∠F=60°,∠ECF=60°,得到△CEF为等边三角形,于是EF=CE=CF,易得AD=EF,AC=DF=AB,根据三角形全等的判定可得到△ABD≌△FDE,即可得到结论.
(2)过E作EF∥BA交AC的延长线于F点,根据等边三角形的性质得到∠A=∠ACB=60°,AB=AC,则∠F=60°,∠ECF=60°,得到△CEF为等边三角形,于是EF=CE=CF,易得AD=EF,AC=DF=AB,根据三角形全等的判定可得到△ABD≌△FDE,即可得到结论.
解答:解:(1)∵在等边△ABC中,D是AC的中点,
∴BD为∠ABC的角平分线,∠ABC=∠ACB=60°
∴∠CBD=
∠ABC=30°,
∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE+∠CED=∠ACB,
∴∠CDE=∠CED=
∠ACB=30°,
∴∠CBD=∠CED=30°,
∴BD=DE;
(2)BD=DE,
证明:过E作EF∥BA交AC的延长线于F点,如图,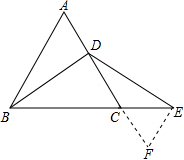
∵△ABC为等边三角形,
∴∠A=∠ACB=60°,AB=AC,
∴∠F=60°,∠ECF=60°,
∴△CEF为等边三角形,
∴EF=CE=CF,
而AD=CE,
∴AD=EF,AC=DF=AB,
在△ABD和△FDE中,
,
∴△ABD≌△FDE(SAS),
∴DB=DE;
∴BD为∠ABC的角平分线,∠ABC=∠ACB=60°
∴∠CBD=
| 1 |
| 2 |
∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE+∠CED=∠ACB,
∴∠CDE=∠CED=
| 1 |
| 2 |
∴∠CBD=∠CED=30°,
∴BD=DE;
(2)BD=DE,
证明:过E作EF∥BA交AC的延长线于F点,如图,

∵△ABC为等边三角形,
∴∠A=∠ACB=60°,AB=AC,
∴∠F=60°,∠ECF=60°,
∴△CEF为等边三角形,
∴EF=CE=CF,
而AD=CE,
∴AD=EF,AC=DF=AB,
在△ABD和△FDE中,
|
∴△ABD≌△FDE(SAS),
∴DB=DE;
点评:本题考查了等边三角形的判定与性质:有两个内角为60°的三角形为等边三角形;等边三角形的三个内角都等于60°,三边都相等.也考查了三角形全等的判定与性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,△ABC以直线m为对称轴的轴对称图形,若BC=8,AD=7,则阴影部分的面积是( )
如图,△ABC以直线m为对称轴的轴对称图形,若BC=8,AD=7,则阴影部分的面积是( )| A、56 | B、28 |
| C、14 | D、无法确定 |
 一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )

 如图,已知在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
如图,已知在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长. 如图所示,在数轴上有三个点,A,B,C,回答下列问题.
如图所示,在数轴上有三个点,A,B,C,回答下列问题.