题目内容
19.解下列方程:(1)$\frac{x+1}{x-5}-\frac{1}{5-x}=4$
(2)$\frac{x}{x+2}-\frac{x+2}{x-2}=\frac{8}{{{x^2}-4}}$.
分析 (1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,据此解答即可,注意最简公分母为x-5.
(2)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,据此解答即可,注意最简公分母为x2-4.
解答 解:(1)方程两边同时乘以x-5,
可得:x+1+1=4(x-5),
解得x=$\frac{22}{3}$,
经检验x=$\frac{22}{3}$是原方程的解,
∴原方程的解是x=$\frac{22}{3}$.
(2)方程两边同时乘以x2-4,
可得:x(x-2)-(x+2)2=8,
整理,可得-6x-4=8,
解得x=-2,
经检验x=-2不是原方程的解,
∴原方程无解.
点评 此题主要考查了解分式方程的方法,要熟练掌握,解答此题的关键是要明确解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,特别注意要检验.

练习册系列答案
相关题目
11.若点P是平面直角坐标系中第二象限内的点,且点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是( )
| A. | (-4,3) | B. | (-3,4) | C. | (3,4) | D. | (4,-3) |
9.下列命题错误的是( )
| A. | 经过三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 同圆或等圆中,相等的圆心角所对的弧相等 | |
| D. | 切线垂直于经过切点的半径 |
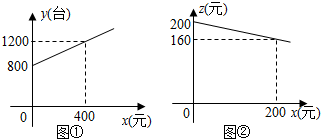 为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.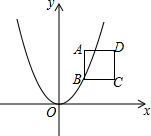 如图,一条抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形ABCD有公共点.
如图,一条抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形ABCD有公共点.