题目内容
7.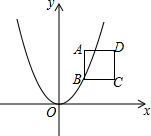 如图,一条抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形ABCD有公共点.
如图,一条抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形ABCD有公共点.(1)求a的取值范围;
(2)若a为整数,求函数的表达式.
分析 (1)根据图形,求出过AC两点的抛物线解析式可确定a的取值范围;
(2)由(1)可知a的取值范围内的整数值,写出函数的表达式即可.
解答 解:(1)∵四条直线x=1,x=2,y=1,y=2围成的正方形ABCD
∴A(1,2),C(2,1),
再根据抛物线的性质,|a|越大开口越小,
把A点代入y=ax2得a=2,
把C点代入y=ax2得a=$\frac{1}{4}$,
则a的范围介于这两点之间,故$\frac{1}{4}$≤a≤2;
(2)∵a为整数且$\frac{1}{4}$≤a≤2,
∴a=1或2,
∴函数的表达式为:y=x2或y=2x2.
点评 本题考查了待定系数法以及学生的观察能力,把函数性质与正方形连接起来,要学会数形结合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.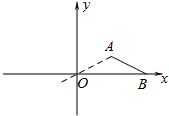 如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )
如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )
 如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )
如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )| A. | (2,1) | B. | (-2,-1) | C. | (-1,2) | D. | (-4,-2) |
19.解下列方程:
(1)$\frac{x+1}{x-5}-\frac{1}{5-x}=4$
(2)$\frac{x}{x+2}-\frac{x+2}{x-2}=\frac{8}{{{x^2}-4}}$.
(1)$\frac{x+1}{x-5}-\frac{1}{5-x}=4$
(2)$\frac{x}{x+2}-\frac{x+2}{x-2}=\frac{8}{{{x^2}-4}}$.
16.下列调查适合作抽样调查的是( )
| A. | 了解中央电视台“星光大道”栏目的收视率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | “神七”载人飞船发射前对重要零部件的检查 |