题目内容
6.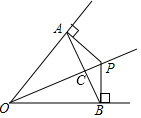 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:①图中有3对全等三角形
②∠CAP=∠COB
③∠OPA=∠OPB
④AB垂直平分OP
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 依据觉平分线的性质可得到AP=PB,然后依据HL可证明△AOP≌△BOP,则OA=OB,然后依据SAS可证明△AOC≌△BOC,则∠OCA=∠OCB=90°,依据HL可证明Rt△APC≌Rt△BPC,依据同角的余角相等可证明∠CAP=∠COB,依据全等三角形的性质可证明∠OPA=∠OPB.
解答 解:∵OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,
∴PA=PB.
在Rt△PAO和Rt△PBO中,$\left\{\begin{array}{l}{PA=PB}\\{OP=OP}\end{array}\right.$,
∴Rt△PAO≌Rt△PBO.
∴OA=OB,∠OPA=∠OPB,故③正确.
在△AOC和△BOC中,$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOC}\\{OC=OC}\end{array}\right.$,
∴△AOC≌△BOC.
∴AC=BC,∠OCA=∠OCB=90°.
∴OP是AB的垂直平分线,故④错误.
在Rt△PAC和Rt△PBC中,$\left\{\begin{array}{l}{CP=CP}\\{AP=BP}\end{array}\right.$,
∴Rt△PAC≌Rt△PBC,故①正确.
∵∠AOP+∠APO=90°,∠PAC+∠APC=90°,
∴∠CAP=∠COB,故②正确.
故选:C.
点评 本题主要考查的是全等三角形的性质和判定、角平分线的性质,熟练掌握全等三角形的性质和判定定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )| A. | 127° | B. | 53° | C. | 127°或53° | D. | 不能确定 |
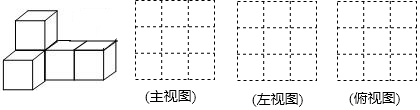
16. 若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
 若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )| A. | 4 | B. | 4.5 | C. | 5 | D. | 5.5 |

 如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.