题目内容
18．
如图，有一块直角三角形纸片，两直角边AC=7cm，BC=24cm，现将直角边AC沿直线AD折叠，使它恰好落在斜边AB上，且与AE重合，求CD的长．
分析 根据折叠的性质可得AC=AE=7cm，CD=DE，∠ACD=∠AED=∠DEB=90°，利用勾股定理列式求出AB，从而求出BE，设CD=DE=x，表示出BD，然后在Rt△DEB中，利用勾股定理列式计算即可得解．
解答 解：∵△ACD与△AED关于AD成轴对称，
∴AC=AE=7cm，CD=DE，∠ACD=∠AED=∠DEB=90°，
在Rt△ABC中，AB2=AC2+BC2=72+242 =252，
∴AB=25，
BE=AB-AE=25-7=18，
设CD=DE=xcm，则DB=BC-CD=24-x，
在Rt△DEB中，由勾股定理，得x2+182=（24-x）2，
解得x=$\frac{21}{4}$，
即CD=$\frac{21}{4}$cm．
点评 本题考查了翻折变换的性质，勾股定理的应用，熟记性质并表示出Rt△DEB的三边，然后利用勾股定理列出方程是解题的关键．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
相关题目
17．计算（$\frac{1}{2}}$）-1所得结果是（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
6．
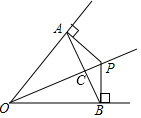如图，OP平分∠AOB，PA⊥OA于A，PB⊥OB于B，连结AB交OP于C，给出下列结论：
①图中有3对全等三角形
②∠CAP=∠COB
③∠OPA=∠OPB
④AB垂直平分OP
其中正确的个数是（ ）
如图，OP平分∠AOB，PA⊥OA于A，PB⊥OB于B，连结AB交OP于C，给出下列结论：①图中有3对全等三角形
②∠CAP=∠COB
③∠OPA=∠OPB
④AB垂直平分OP
其中正确的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
13．下列说法正确的是（ ）
| A． | “x2＜0（x是实数）”是随机事件 | |
| B． | “打开电视，正在播放《新闻联播》”是必然事件 | |
| C． | “射击运动员射击一次，命中靶心”是随机事件 | |
| D． | “经过由交通信号灯的路口，遇到红灯”是必然事件 |
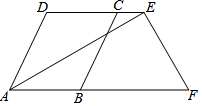已知如图：AD∥BC，E、F分别在DC、AB延长线上．∠DCB=∠DAB，∠DEA=30°，AE⊥EF，垂足为E．