题目内容
1.学校为了响应国家阳光体育活动,选派部分学生参加足球、乒乓球、篮球、排球队集训.根据参加项目制成如下两幅不完整的统计图(要求每位同学只能选择一种自己喜欢的球类,图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数,请你根据图中提供的信息解答下列问题:
(1)参加篮球队的有人,参加足球队的人数占全部参加人数的%.
(2)喜欢排球队的人数在扇形统计图中所占的圆心角是多少度?并补全频数分布折线统计图.
(3)若足球队只剩一个集训名额,学生小明和小虎都想参加足球队,决定采用随机摸球的方式确定参加权,具体规则如下:一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球,小明随机地从四个小球中摸出一球然后放回,小虎再随机地摸出一球,若小明摸出的小球标有数字比小虎摸出的小球标有的数字大,则小明参加;若小明摸出的小球标有数字比小虎摸出的小球标有的数字小,则小虎参加,试分析这种规则对双方是否公平?
分析 (1)根据折线图与扇形图首先得出参加乒乓球队的人数与百分比得出总人数,再利用扇形图即可得出参加篮球的人数,以及参加足球对的人数占全部参加人数的百分比;
(2)根据喜欢排球队的人数在扇形统计图中所占的圆心角是百分比为:1-(40%+30%+20%)=10%,即可得出所占的圆心角的度数,即可补全图形;
(3)利用树状图画出即可得出小虎获参加权的概率以及小明获参加权的概率得出即可.
解答 解:(1)∵结合折线图与扇形图得出参加乒乓球队的人数为20,占总数的20%,
∴总人数为:20÷20%=100人,
∴参加篮球队的有:100×40%=40人,
参加足球队的人数占全部参加人数的:30÷100×100%=30%,
故答案为:40,30;
(2)喜欢排球队的人数在扇形统计图中所占的圆心角是百分比为:1-(40%+30%+20%)=10%,
圆心角度数=360×10%=36°;正确补全折线图中篮球、排球折线;
(3)用列表法
| 小虎 小明 | 1 | 2 | 3 | 4 |
| 1 | 1,1 | 1,2 | 1,3 | 1,4 |
| 2 | 2,1 | 2,2 | 2,3 | 2,4 |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 |
分别是2,1;3,1;3,2;4,1;4,2;4,3;
∴小明获参加权的概率P1=$\frac{6}{16}$=$\frac{3}{8}$,小虎获参加权的概率P2=$\frac{6}{16}$=$\frac{3}{8}$
∵P1=P2,
∴这个规则对双方公平.
点评 此题主要考查了游戏的公平性以及列表法求概率,结合题意正确的列出图表是考查重点,同学们应熟练掌握此知识.

练习册系列答案
相关题目
1.计算(-1)2的正确结果是( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
6.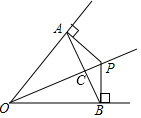 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
①图中有3对全等三角形
②∠CAP=∠COB
③∠OPA=∠OPB
④AB垂直平分OP
其中正确的个数是( )
 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:①图中有3对全等三角形
②∠CAP=∠COB
③∠OPA=∠OPB
④AB垂直平分OP
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列说法正确的是( )
| A. | “x2<0(x是实数)”是随机事件 | |
| B. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| C. | “射击运动员射击一次,命中靶心”是随机事件 | |
| D. | “经过由交通信号灯的路口,遇到红灯”是必然事件 |
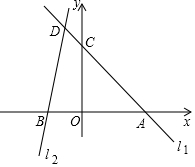 如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)
如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)