题目内容
 如图矩形ABCD中,AB=2,点E在BC上并且AE=EC,若将矩形纸片沿AE折叠,使点B恰好落在AC上,则矩形ABCD的面积为( )
如图矩形ABCD中,AB=2,点E在BC上并且AE=EC,若将矩形纸片沿AE折叠,使点B恰好落在AC上,则矩形ABCD的面积为( )A、
| ||
B、2
| ||
C、4
| ||
D、6
|
考点:翻折变换(折叠问题)
专题:探究型
分析:根据折叠的性质及等边对等角的性质,可得到∠BAE=∠EAC=∠ECA,根据三角形内角和定理即可求得∠ECA的度数,再根据直角三角形的性质可求得AC的长,在Rt△ABC中利用勾股定理可求出BC的长,根据矩形的面积公式即可得出结论.
解答:解:∵AE=EC,
∴∠EAC=∠ECA,
∵将纸片沿AE折叠,点B恰好落在AC上,
∴∠BAE=∠EAC,
∴∠BAE=∠EAC=∠ECA,
∵∠B+∠ECA+∠CAB=180°,
∴∠ECA=30°,
∵AB=2,
∴AC=2AB=4,
在Rt△ABC中,
∵AB2+BC2=AC2,即22+BC2=42,解得BC=2
,
∴S矩形ABCD=AB•BC=2×2
=4
.
故选C.
∴∠EAC=∠ECA,
∵将纸片沿AE折叠,点B恰好落在AC上,
∴∠BAE=∠EAC,
∴∠BAE=∠EAC=∠ECA,
∵∠B+∠ECA+∠CAB=180°,
∴∠ECA=30°,
∵AB=2,
∴AC=2AB=4,
在Rt△ABC中,
∵AB2+BC2=AC2,即22+BC2=42,解得BC=2
| 3 |
∴S矩形ABCD=AB•BC=2×2
| 3 |
| 3 |
故选C.
点评:本题考查的是图形的反折变换及矩形的性质,熟知图形反折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
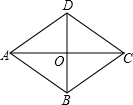 如图,在菱形ABCD中,对角线AC和BD相交于O点,若OA=4,OB=3,则菱形ABCD的周长是( )
如图,在菱形ABCD中,对角线AC和BD相交于O点,若OA=4,OB=3,则菱形ABCD的周长是( )| A、5 | B、12 | C、16 | D、20 |
方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知点A(x1,6),B(x2,-2),C(x3,-4)都是反比例函数y=-
(a≠0)图象上的点,则x1,x2,x3的大小关系是( )
| a2 |
| x |
| A、x1<x2<x3 |
| B、x1<x3<x2 |
| C、x3<x2<x1 |
| D、x2<x3<x1 |

 八年级若干名学生参加“学雷峰活动”的歌唱比赛,比赛成绩的频数分布直方图如图,请根据这个直方图回答下面的问题:
八年级若干名学生参加“学雷峰活动”的歌唱比赛,比赛成绩的频数分布直方图如图,请根据这个直方图回答下面的问题: 如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-10x+24=0的两个根,则DE的长为
如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-10x+24=0的两个根,则DE的长为