题目内容
1.已知关于x的不等式组$\left\{\begin{array}{l}x-a≥0\\ 5-2x>1\end{array}\right.$只有四个整数解,则实数a的取值范是-3<a≤-2.分析 首先解不等式组,即可确定不等式组的整数解,即可确定a的范围.
解答 解:$\left\{\begin{array}{l}{x-a≥0…①}\\{5-2x>1…②}\end{array}\right.$,
解①得:x≥a,
解②得:x<2.
∵不等式组有四个整数解,
∴不等式组的整数解是:-2,-1,0,1.
则实数a的取值范围是:-3<a≤-2.
故答案是:-3<a≤-2.
点评 本题考查了不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
12.若反比例函数y=$\frac{2m-1}{x}$,y随x的增大而减小,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m<$\frac{1}{2}$ | C. | m>-$\frac{1}{2}$ | D. | m<-$\frac{1}{2}$ |
6.解下列不等式组,结果正确的是( )
| A. | 不等式组$\left\{{\begin{array}{l}{x>7}\\{x>3}\end{array}}\right.$的解集是x>3 | |
| B. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x>-2}\end{array}}\right.$的解集是-3<x<-2 | |
| C. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x<-1}\end{array}}\right.$的解集是x<-1 | |
| D. | 不等式组$\left\{{\begin{array}{l}{x>-4}\\{x<2}\end{array}}\right.$的解集是-4<x<2 |
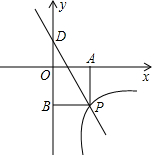 如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数y=$\frac{m}{x}$的图象在第四象限的相交于点P,并且PAx轴于点A,PB⊥y轴于点B,已知B(0,-6),且S△DBP=27
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数y=$\frac{m}{x}$的图象在第四象限的相交于点P,并且PAx轴于点A,PB⊥y轴于点B,已知B(0,-6),且S△DBP=27 一次函数y=$\frac{3}{2}$x-3
一次函数y=$\frac{3}{2}$x-3