题目内容
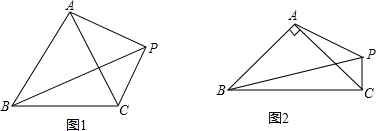
如图，在四边形形ABCD中，∠ADB=∠DBC=90°，AD=6，sinA=| 4 |
| 5 |
考点：解直角三角形
专题：计算题
分析：先在Rt△ADB中利用∠A的正弦得到sinA=
=
，则可设BD=4x，AB=5x，根据勾股定理计算出AD=3x，所以3x=6，解得x=2，则BD=8，再在Rt△BCD中根据勾股定理计算出CD=4
，然后根据锐角三角函数的定义求解．
| BD |
| AB |
| 4 |
| 5 |
| 13 |
解答：解：在Rt△ADB中，∵sinA=
=
，
∴设BD=4x，则AB=5x，
∴AD=
=3x，
而AD=6，
∴3x=6，解得x=2，
∴BD=4x=8，
在Rt△BCD中，∵BD=8，BC=12，
∴CD=
=4
，
∴sinC=
=
=
，
cosC=
=
=
，
tanC=
=
=
．
| BD |
| AB |
| 4 |
| 5 |
∴设BD=4x，则AB=5x，
∴AD=
| (5x)2-(4x)2 |
而AD=6，
∴3x=6，解得x=2，
∴BD=4x=8，
在Rt△BCD中，∵BD=8，BC=12，
∴CD=
| BD2+BC2 |
| 13 |
∴sinC=
| BD |
| CD |
| 8 | ||
4
|
2
| ||
| 13 |
cosC=
| BC |
| CD |
| 12 | ||
4
|
3
| ||
| 13 |
tanC=
| BD |
| CB |
| 8 |
| 12 |
| 2 |
| 3 |
点评：考查了解直角三角形的定义：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
相关题目
如图所示的抛物线二次函数y=ax2-3x+a2-a-2的图象，那么a的值是要使式子
有意义，则x的取值范围是（ ）
| 1-x |
| A、x≤1 | B、x≥1 |
| C、x＞0 | D、x＞-1 |
若函数y=mx2+（m+2）x的图象与x轴只有一个交点，那么m的值为（ ）
| A、-2 | B、0或2 |
| C、2或-2 | D、0或-2 |
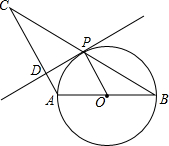如图，△ABC中，AB=AC，以AB为直径的圆O交BC于点P，PD⊥AC于点D
如图，在△ABC中，DE∥AB，BE：EC=1：2，AB=6cm，求DE的长．