题目内容
如图，在△ABC中，DE∥AB，BE：EC=1：2，AB=6cm，求DE的长．考点：相似三角形的判定与性质
专题：
分析：由BE：EC=1：2可得EC：BC=2：3，且由平行可得EC：BC=DE：AB，代入可求得DE．
解答：解：
∵BE：EC=1：2，
∴EC：BC=2：3，
∵DE∥AB，
∴EC：BC=DE：AB，且AB=6cm，
∴DE：6=2：3，
解得DE=4cm．
∵BE：EC=1：2，
∴EC：BC=2：3，
∵DE∥AB，
∴EC：BC=DE：AB，且AB=6cm，
∴DE：6=2：3，
解得DE=4cm．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段中的线段对应成比例是解题的关键．
练习册系列答案
相关题目
如图，在四边形形ABCD中，∠ADB=∠DBC=90°，AD=6，sinA=在直角坐标系内，已知A、B两点的坐标分别为A（0，1）、B（3，2），M为x轴上一点，且MA+MB最小，则M的坐标是（ ）
| A、（0，0） |
| B、（1，0） |
| C、（2，0） |
| D、（3，0） |
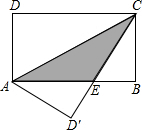如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，CD落在AB上的点为E点，则重叠部分△AEC的面积是多少？
已知，如图，AB=CD，AE=CF，BE=DF，求证：AF∥CE．
如图，AC=CD=DB，CM=DM，写出图中哪一个点是哪一条线段的中点．