题目内容
若函数y=mx2+(m+2)x的图象与x轴只有一个交点,那么m的值为( )
| A、-2 | B、0或2 |
| C、2或-2 | D、0或-2 |
考点:抛物线与x轴的交点
专题:
分析:分m≠0,m=0两种情况讨论,进而求出m的值得出答案即可.
解答:解:当m=0,则函数y=mx2+(m+2)x是一次函数关系,
故图象一定x轴有一个交点,
当m≠0,
∵y=mx2+(m+2)x的图象与x轴只有一个交点,
∴b2-4ac=(m+2)2=0,
解得:m1=m2=-2,
综上所述:m=0或-2.
故选:D.
故图象一定x轴有一个交点,
当m≠0,
∵y=mx2+(m+2)x的图象与x轴只有一个交点,
∴b2-4ac=(m+2)2=0,
解得:m1=m2=-2,
综上所述:m=0或-2.
故选:D.
点评:此题主要考查了抛物线与x轴交点问题,利用分类讨论得出是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
若k为整数,则使方程(k-3)x=2013-4x的解也是整数的k的值有( ) 个.
| A、16 | B、12 | C、9 | D、8 |
 如图,在四边形形ABCD中,∠ADB=∠DBC=90°,AD=6,sinA=
如图,在四边形形ABCD中,∠ADB=∠DBC=90°,AD=6,sinA=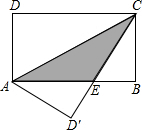 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少?
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少? 如图,直线AB、CD交于点O,且∠EOD=65°,∠COF=130°,OB平分∠DOF,问EO与直线AB的位置关系如何?请说明理由.
如图,直线AB、CD交于点O,且∠EOD=65°,∠COF=130°,OB平分∠DOF,问EO与直线AB的位置关系如何?请说明理由.