题目内容
2.求分式(x-2-$\frac{{x}^{2}-x}{x+2}$)÷$\frac{x-4}{2}$的值,其中x取不等式组$\left\{\begin{array}{l}{2x<-1}\\{x+2>0}\end{array}\right.$的整数解.分析 根据分式的运算法则进行化简,然后根据不等式组解出x的值.
解答 解:由不等式组可得:-2<x<-$\frac{1}{2}$
其整数解为:x=-1
原式=$\frac{{x}^{2}-4-{x}^{2}+x}{x+2}$•$\frac{2}{x-4}$
=$\frac{x-4}{x+2}$•$\frac{2}{x-4}$
=$\frac{2}{x+2}$
=2
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.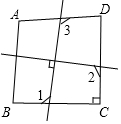 如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
 如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )
如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( )| A. | ∠1=∠2>∠3 | B. | ∠1=∠3>∠2 | C. | ∠2>∠1=∠3 | D. | ∠3>∠1=∠2 |
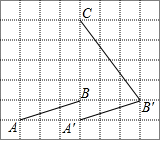 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上,向右平移线段AB至A'B'(A对应点为A').
如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上,向右平移线段AB至A'B'(A对应点为A').
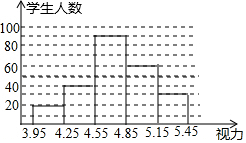 近年来“低头族”现象日趋严重,初中生的视力状况受到了全社会的广泛关注.某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,并利用所得的数据绘制了如图的频数分布直方图,根据图中提供的信息解答下列问题:
近年来“低头族”现象日趋严重,初中生的视力状况受到了全社会的广泛关注.某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,并利用所得的数据绘制了如图的频数分布直方图,根据图中提供的信息解答下列问题: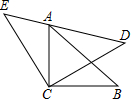 如图,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在ECD的斜边DE上,求证:AE2+AD2=2AC2.
如图,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在ECD的斜边DE上,求证:AE2+AD2=2AC2. 如图,已知AB⊥BC,BC⊥CD,BE∥CF,∠ABE=50°,求∠FCD的度数.
如图,已知AB⊥BC,BC⊥CD,BE∥CF,∠ABE=50°,求∠FCD的度数.