题目内容
12.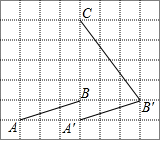 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上,向右平移线段AB至A'B'(A对应点为A').
如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上,向右平移线段AB至A'B'(A对应点为A').(1)当AA'=3时,计算A'C+B'C的值等于9;
(2)当A'C+B'C取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段A'B',并简要说明点A'和B'的位置是如何找到的(不要求证明).
分析 (1)观察图象,利用勾股定理即可解决问题;
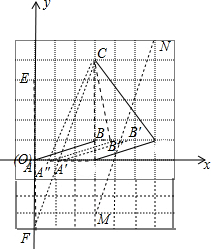
(2)如图建立如图坐标系,设AA″=BB″=x,则A′C+CB′=$\sqrt{(3-x)^{2}}$+$\sqrt{{x}^{2}+{4}^{2}}$欲求A′C+CB′的最小值,可以看作在轴上一点A′使得A′到E(0,4),C(3,5)的距离之和的最小值,取F(0,-4),连接CF交x轴于A′,点A′即为所求,同法取N(6,6),M(3,3),连接NM可得B′;
解答 解:(1)由图象可知,A′C=5,B′C=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴A′C+B′C=9,
故答案为9.
(2)如图建立如图坐标系,设AA″=BB″=x,
则A′C+CB′=$\sqrt{(3-x)^{2}}$+$\sqrt{{x}^{2}+{4}^{2}}$
欲求A′C+CB′的最小值,可以看作在轴上一点A′使得A′到E(0,4),C(3,5)的距离之和的最小值,
取F(0,-4),连接CF交x轴于A′,点A′即为所求,同法取N(6,6),M(3,3),连接NM可得B′.
,
点评 本题考查作图-平移变换,坐标与图形的性质,轴对称、两点之间线段最短等知识,解题的关键是学会用转化的思想思考问题,体现了数形结合的思想,学会利用轴对称解决最值问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.下列分式的变形不正确的是( )
| A. | $\frac{-(a+b)}{c}$=-$\frac{a+b}{c}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | C. | $\frac{-a-b}{c}$=-$\frac{a+b}{c}$ | D. | $\frac{b-a}{-c}$=$\frac{a-b}{c}$ |
1.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-2a2)3=-8a6 | C. | (a+b)2=a2+b2 | D. | 2a+3a=5a2 |
 将正整数按如下规律排列,若2016在第n行第m列,则n=672,m=2.
将正整数按如下规律排列,若2016在第n行第m列,则n=672,m=2.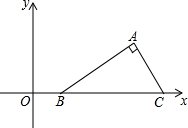 在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,点B的坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕点B顺时针旋转180°,然后向下平移2个单位,则点A的对应点D的坐标为(-2,-2-$\sqrt{3}$).
在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,点B的坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕点B顺时针旋转180°,然后向下平移2个单位,则点A的对应点D的坐标为(-2,-2-$\sqrt{3}$).
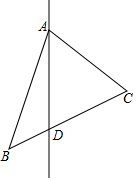 如图.已知△ABC.点D在BC边上.过点A作直线AD.
如图.已知△ABC.点D在BC边上.过点A作直线AD.