题目内容
已知反比例函数y=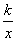 (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=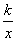 (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
(1)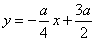 ;(2)10<S<16.
;(2)10<S<16.
【解析】
试题分析:(1)先把点A(2,a)代入反比例函数y=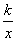 (x>0)求出k的值,再根据F为线段的中点可知F的纵坐标为
(x>0)求出k的值,再根据F为线段的中点可知F的纵坐标为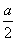 ,把y=
,把y=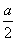 代入y=
代入y=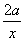 可得出x的值,进而得出点F的坐标,利用待定系数求出直线AF的解析式即可;
可得出x的值,进而得出点F的坐标,利用待定系数求出直线AF的解析式即可;
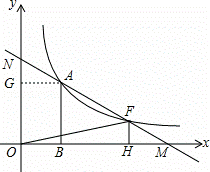
(2)根据点F(p,q) 在反比例函数y=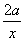 的图象上且q=-a2+5a可得出F点的坐标,故可得出直线AF的解析式,进而得出M、N的坐标,过A作AG⊥y轴于点G,则可得出AG,ON,OM,FH的长,根据S=S△ANO+S△MFO=
的图象上且q=-a2+5a可得出F点的坐标,故可得出直线AF的解析式,进而得出M、N的坐标,过A作AG⊥y轴于点G,则可得出AG,ON,OM,FH的长,根据S=S△ANO+S△MFO=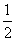 •ON•AG+
•ON•AG+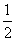 OM•FH可得出关于S、a的二次函数,根据a的取值范围即可得出结论.
OM•FH可得出关于S、a的二次函数,根据a的取值范围即可得出结论.
试题解析:(1)∵反比例函数y=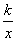 (x>0)的图象经过点A(2,a)(a>0),
(x>0)的图象经过点A(2,a)(a>0),
∴k=2a,
∴y=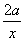 ,
,
∵F为线段的中点,
∴F的纵坐标为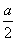 ,把y=
,把y=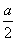 代入y=
代入y=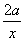 得x=4
得x=4
∴F(4,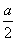 ),
),
设直线AF的解析式为y=k1x+b,
∴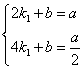 ,
,
解得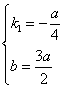 ,
,
∴直线AF的解析式为: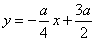 ;
;
(2)∵F(p,q) 在反比例函数y=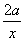 的图象上,
的图象上,
∴q=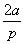 ,
,
∵q=-a2+5a,
∴p=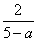 ,
,
∴F(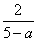 ,-a2+5a)
,-a2+5a)
∴直线AF的解析式为:y=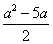 x+(6a-a2),
x+(6a-a2),
∴N(0,6a-a2),M(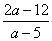 ,0),
,0),
过A作AG⊥y轴于点G,
则AG=2,ON=6a-a2,OM=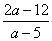 ,FH=-a2+5a
,FH=-a2+5a
S=S△ANO+S△MFO=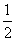 •ON•AG+
•ON•AG+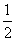 OM•FH
OM•FH
=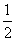 ×2×(6a-a2)+
×2×(6a-a2)+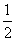 •
•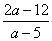 •(-a2+5a)
•(-a2+5a)
=-2a2+12a
=-2(a-3)2+18
∵q>0,q<a,
∴4<a<5.
∴由函数性质可知,10<S<16.
【难度】困难

 科学实验活动册系列答案
科学实验活动册系列答案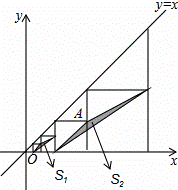
 ,
, ,其中
,其中 为锐角,求证:
为锐角,求证: 。
。

 的图象相交于点(2,a).
的图象相交于点(2,a).
 a
a (B)
(B)  (C)
(C)  (D)
(D) 
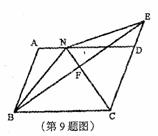
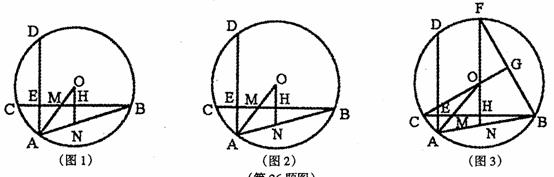 ⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=
⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=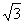 , 求⊙0的半径长.
, 求⊙0的半径长.  ,则t的值为
,则t的值为 