题目内容
已知:AD、BC是⊙O的两条互相垂直的弦,垂足为E,H是弦BC的中点,AO是 ∠DAB的平分线,半径OA交弦CB于点M.
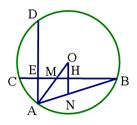
(1)如图1,延长OH交AB于点N,求证:ONB=2ZAON;
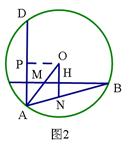
(2)如图2,若点M是OA的中点,求证:AD=40H;
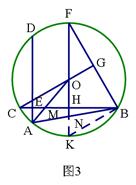
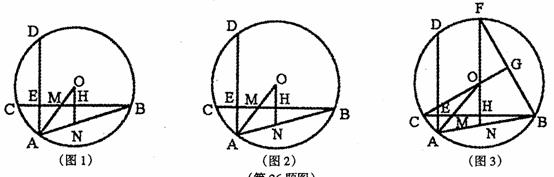 ⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=
⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=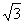 , 求⊙0的半径长.
, 求⊙0的半径长.
(1)证明:如图1,H是弦BC的中点,
∴AD⊥BC ∴∠DEB=90°
∴∠OHB=∠DEB ∴OH∥AD ∴∠DAO=∠AOH ……1分
∵∠DAO=∠OAN ∴ ∠OAN=∠NOA ……1分
∴∠ONB=∠NAO+∠NOA=2∠AON
 ∴∠ONB=2∠AON; ……1分
∴∠ONB=2∠AON; ……1分
(2) 如图2,过点O作OP⊥AD,可证四边形OHEP是矩形
∴OH=EP ∵点M是OA的中点,可证△OHM≌△AEM
∴OH=AE ∴EP=AE ……1分
即:AP=2AE=2OH
∵OP⊥AD ∴AD=2AP ……1分
 |
∴AD=2AP=2×2OH=4OH
∴AD=4OH ……1分
(3)如图3,延长FN交⊙O于点K,连接BK,
∵FK是⊙O的直径 ∴∠KBF=90°
∵CG⊥BF, ∴∠CGF=90°∴CG∥BK ……1分
∴ ∠CON=∠OKB 又∵∠COK=2∠CBK
 ∴∠OKB=2∠CBK ……1分
∴∠OKB=2∠CBK ……1分
在Rt△HKB中,∠CBK+∠OKB=90°
∴ ∠CBK=30°,∴∠COK=2∠CBK=60° ……1分
在Rt△OCH中,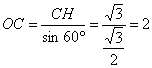
∴⊙O的半径为2. ……1分

练习册系列答案
相关题目

 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .

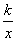 (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= ,其中a=2tan60°,b=2cos30°
,其中a=2tan60°,b=2cos30°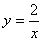 的图象上,若x1<0 <x2,则y1、y2
的图象上,若x1<0 <x2,则y1、y2 ( )A.
( )A. ;B.
;B. ;C.
;C. ;D.
;D. 。
。